题目内容
10．已知双曲线y=$\frac{2}{3x}$（x＞0）上一点P，则P点到原点最近的距离为$\frac{2\sqrt{3}}{3}$．分析 由题意可知点P应在直线y=x上时，点P到原点的距离最近，故设点P的坐标为（x，y），则xy=$\frac{2}{3}$，由x=y，可得x=y=$\frac{\sqrt{6}}{3}$，再利用勾股定理即可求得答案．
解答 解：由题意可知点P应在直线y=x上时，点P到原点的距离最近，
设点P的坐标为（x，y），
∴xy=$\frac{2}{3}$，
即x2=$\frac{2}{3}$，
∵点P在第一象限内，
∴x=y=$\frac{\sqrt{6}}{3}$，
∴点P点到原点最近的距离为$\sqrt{{（\frac{\sqrt{6}}{3}）}^{2}{+（\frac{\sqrt{6}}{3}）}^{2}}$=$\frac{2\sqrt{3}}{3}$，
故答案为：$\frac{2\sqrt{3}}{3}$．
点评 本题主要考查反比例函数图象上的点的特点，得到点P在直线x=y上是解题的关键．
练习册系列答案
相关题目
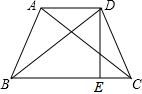如图，在等腰梯形ABCD中，AD∥BC，DE⊥BC于E，若DE=3，BD=5，求梯形ABCD的面积．
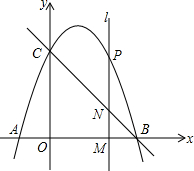如图，直线BC交x轴、y轴于点B（3，0）和C（0，3），且抛物线y=-x2+bx+c过B、C两点，与x轴交于另一点A．
15．已知反比例函数的图象经过（1，-2），则下列各点中，在反比例函数图象上的是（ ）
| A． | （2，1） | B． | $（{\frac{2}{3}，3}）$ | C． | （-2，-1） | D． | （-1，2） |