题目内容
17.(1)$\sqrt{1\frac{2}{3}}$÷2$\sqrt{2\frac{1}{3}}$×(-4$\sqrt{1\frac{2}{5}}$)(2)$\frac{1}{\sqrt{2}}$-$\sqrt{6}$($\sqrt{3}$-2$\sqrt{2}$)
(3)$\frac{\sqrt{3{a}^{2}}}{2b}$•$\sqrt{\frac{a}{b}}$÷2$\sqrt{\frac{2}{b}}$.
分析 (1)根据二次根式的乘除法则运算;
(2)先计算分母有理化和二次根式的乘法运算,然后合并即可;
(3)根据二次根式的乘除法则运算.
解答 解:(1)原式=1×$\frac{1}{2}$×(-4)×$\sqrt{\frac{5}{3}×\frac{3}{7}×\frac{7}{5}}$
=-2;
(2)原式=$\frac{\sqrt{2}}{2}$-3$\sqrt{2}$+4$\sqrt{3}$
=-$\frac{5\sqrt{2}}{2}$+4$\sqrt{3}$;
(3)原式=$\frac{1}{2b}$•$\frac{1}{2}$•$\sqrt{3{a}^{2}•\frac{a}{b}•\frac{b}{2}}$
=$\frac{a\sqrt{6a}}{8b}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
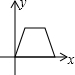
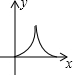
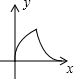
 如图,△ABC与△DEF均为等腰三角形,且△ABC≌△DEF,∠B=∠DEF=90°,点B、C、E、F(C与E重合)在同一条直线上,△ABC从点C出发,沿射线BC方向匀速运动,△DEF的位置保持不动,当点B与点F重合时停止运动.设两个三角形重合部分的面积为y,△ABC平移的距离为x,下面能大致表示y与x间函数关系的图象是( )
如图,△ABC与△DEF均为等腰三角形,且△ABC≌△DEF,∠B=∠DEF=90°,点B、C、E、F(C与E重合)在同一条直线上,△ABC从点C出发,沿射线BC方向匀速运动,△DEF的位置保持不动,当点B与点F重合时停止运动.设两个三角形重合部分的面积为y,△ABC平移的距离为x,下面能大致表示y与x间函数关系的图象是( )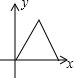
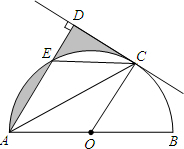 如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE.
如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE.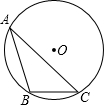 如图,△ABC内接于⊙O,∠A=30°,BC=4cm,求⊙O的直径是8cm.
如图,△ABC内接于⊙O,∠A=30°,BC=4cm,求⊙O的直径是8cm.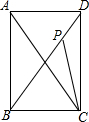 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.
如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.