题目内容
6.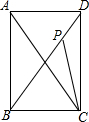 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.
如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.
分析 先根据正方形的性质得∠DBC=∠ACB=45°,再根据等腰三角形的性质和三角形内角和定理得到∠BPC=∠BCP=$\frac{1}{2}$(180°-45°)=67.5°,然后利用∠ACP=∠BCP-∠ACB可计算出∠ACP.
解答 解:∵四边形ABCD为正方形,
∴∠DBC=∠ACB=45°,
∵BP=BC,
∴∠BPC=∠BCP=$\frac{1}{2}$(180°-45°)=67.5°,
∴∠ACP=∠BCP-∠ACB=67.5°-45°=22.5°.
故答案为67.5,22.5.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.
两条对角线将正方形分成四个全等的等腰直角三角形.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
11.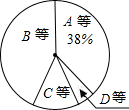 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
(1)试直接写出x=12,y=0.02;
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | ||
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | ||
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
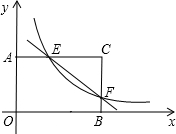 已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=$\frac{k}{x}$(k>0)的图象与AC边交于点E.
已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=$\frac{k}{x}$(k>0)的图象与AC边交于点E.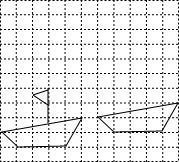 (1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上.
(1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上.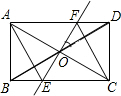 如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交 BC于点E,交AD于点F.若四边形AECF恰好为菱形,则∠FOD=30°.
如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交 BC于点E,交AD于点F.若四边形AECF恰好为菱形,则∠FOD=30°.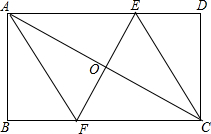 如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.
如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.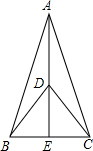 如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE.
如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE.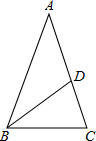 如图,已知:在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ADB的度数是108°.
如图,已知:在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ADB的度数是108°.