题目内容
2.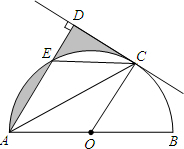 如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE.
如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE.(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,菱形AOCE,求阴影部分面积.
分析 (1)由OA=OC得∠OCA=∠OAC,由AC平分∠DAB得∠DAC=∠OAC,则∠ADC=∠OCA,根据平行线的判定得OC∥AD,由于AD⊥CD,根据平行线的性质得到OC⊥CD,然后根据切线的判定定理即可得到CD是⊙O的切线;
(2)由菱形的性质得到CE=OC=OE=1,△OCE都为等边三角形,得到∠COE=∠OCE=60°,易得∠DCE=30°,在Rt△DCE中,根据含30度的直角三角形三边的关系得DE、DC,所以易求S△DCE,由于弓形AE的面积=弓形CE的面积,所以S阴影=S△DCE.
解答 (1)证明:∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠ADC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结OE,如图,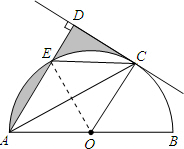
∵四边形OAEC为菱形,
∴CE=OC=OE=2,
∴△OCE都为等边三角形,
∴∠COE=∠OCE=60°,
而∠DCO=90°,
∴∠DCE=30°,
在Rt△DCE中,CE=1,
∴DE=$\frac{1}{2}$CE=$\frac{1}{2}$,DC=$\frac{\sqrt{3}}{2}$CE=$\frac{\sqrt{3}}{2}$,
∴S△DCE=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{8}$,
∵AE弧=CE弧,
∴弓形AE的面积=弓形CE的面积,
∴S阴影=S△DCE=$\frac{\sqrt{3}}{8}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了扇形的面积公式.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
12.一根铁丝正好可以围成一个长是(2a+3b),宽是(a+b)的长方形框,把从这个长方形框上剪去的一段铁丝围成一个长是a,宽是b的长方形框(均不计接缝),则剩下的铁丝长是( )
| A. | a+2b | B. | b+2a | C. | 4a+6b | D. | 6a+4b |
11.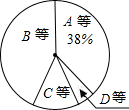 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
(1)试直接写出x=12,y=0.02;
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | ||
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | ||
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
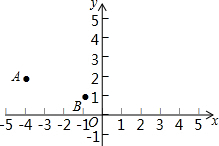 如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,求点P的坐标.
如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,求点P的坐标. 如图,?ABCD的一边AB为直径的⊙O过点C,连结OC,若∠AOC=80°,则∠BCD=140度.
如图,?ABCD的一边AB为直径的⊙O过点C,连结OC,若∠AOC=80°,则∠BCD=140度.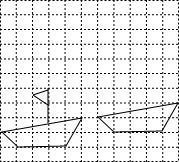 (1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上.
(1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上. 按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.
按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.