题目内容
13．我市某工艺厂设计了一款工艺品投放市场进行试销，通过试销得出该工艺品每天获得的利润是W（元）与销售单价x（元）之间的函数表达式为W=-10（x-40）2+9000，物价部门规定该工艺品的销售单价最高不超过35元，则销售单价定为35元时，工艺厂试销该工艺品每天获得的利润最大，最大利润为8750元．分析 因为x≤35，利用二次函数的增减性，结合对称轴即可得出答案．
解答 解：∵函数W=-10（x-40）2+9000，
∵x≤35，当x≤35时，W的值随着x值的增大而增大，
∴销售单价定为35元∕件时，工艺厂试销该工艺品每天获得的利润最大，
最大利润为8750元．
故答案为：35，8750．
点评 此题主要考查了二次函数的应用，根据函数的增减性求出函数的最值是解题关键．
练习册系列答案
相关题目
如图，已知关于x的二次函数y=x2+mx的图象经过原点O，并且与x轴交于点A，对称轴为直线x=1．若关于x的一元二次方程x2+mx-k=0（k为常数）在-2＜x＜3的范围内有解，则k的取值范围-1≤k＜8．
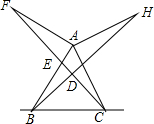如图，已知AF=AB，AF⊥AB，AH=AC，AH⊥AC，连接CF，BH交于点D，求证：
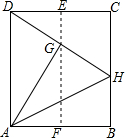如图，在一张长方形纸片ABCD中，AD=25cm，AB=20cm，点E，F分别是CD和AB的中点．现将这张纸片按图示方式折叠，求∠DAH的大小及EG的长（精确到0.1cm）．
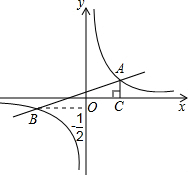如图，已知在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=$\frac{m}{x}$ （m≠0）的图象相交于A、B两点，且点B的纵坐标为-$\frac{1}{2}$，过点A作AC⊥x轴于点C，且AC=1，OC=2．求：
如图，在△ABC中，∠ACB=90°，CD⊥AB于D，∠A=30°，E为AB的中点，则∠ECD=30°．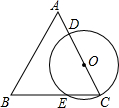
如图，△ABC是等边三角形，点O在边AC上（不与A，C重合），以点O为圆心，以OC为半径的圆分别与AC、BC相交于点D、E，若OC=1，则$\widehat{DE}$的长是$\frac{2π}{3}$（结果保留π）．