题目内容
8.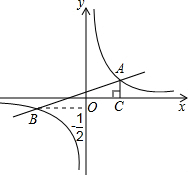 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$ (m≠0)的图象相交于A、B两点,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴于点C,且AC=1,OC=2.求:
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$ (m≠0)的图象相交于A、B两点,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴于点C,且AC=1,OC=2.求:(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)连接AO、BO,求△ABO的面积.
分析 (1)首先由点的坐标的意义,得出点A的坐标,然后把点A的坐标代入反比例函数的解析式y=$\frac{m}{x}$,中,求出m的值,从而得出反比例函数的解析式;
(2)首先由点B在反比例函数y=$\frac{m}{x}$的图象上,可求出点B的坐标,然后根据点A、点B都在一次函数y=kx+b(k≠0)的图象上,利用待定系数法求出一次函数的解析式;
(3)根据直线y=$\frac{1}{4}$x+$\frac{1}{2}$与y轴的交点(0,$\frac{1}{2}$),即可得到结论.
解答 解:(1)依题意,知点A的坐标是(2,1).
∵点A在反比例函数y=$\frac{m}{x}$ (m≠0)的图象上,
∴m=2×1=2.
∴反比例函数的解析式为y=$\frac{2}{x}$;
(2)∵y=$\frac{2}{x}$,
∴当y=-$\frac{1}{2}$时,x=-4.
∴点B的坐标为(-4,-$\frac{1}{2}$).
∵点A、点B都在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}{2k+b=1}\\{-4k+b=-\frac{1}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=\frac{1}{2}}\end{array}\right.$.
∴一次函数的解析式为y=$\frac{1}{4}$x+$\frac{1}{2}$;
(3)在y=$\frac{1}{4}$x+$\frac{1}{2}$中,令x=0,得y=$\frac{1}{2}$,
∴直线y=$\frac{1}{4}$x+$\frac{1}{2}$与y轴的交点(0,$\frac{1}{2}$),
∴S△AOB=$\frac{1}{2}×$$\frac{1}{2}$×$\frac{1}{2}$+$\frac{1}{2}×\frac{1}{2}$×2=$\frac{5}{8}$.
点评 本题考查了反比例函数和一次函数的交点问题,函数解析式的求法,三角形面积的求法,熟练掌握函数解析式的求法是解题的关键.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案| A. | 相切 | B. | 相离 | C. | 相切或相交 | D. | 相离或相切 |
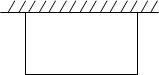 (1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大?
(1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大? 如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=8,则DE=3.
如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=8,则DE=3.