题目内容
2.把下列各式分母有理化:(1)$\frac{2(a-1)}{\sqrt{2a+4}}$
(2)$\frac{1}{\sqrt{2}-1}$
(3)$\frac{3\sqrt{5}-2\sqrt{3}}{3\sqrt{5}+2\sqrt{3}}$.
分析 找出各项的有理化因式,分子分母分别乘以有理化因式,计算即可得到结果.
解答 解:(1)原式=$\frac{2(a-1)\sqrt{2a+4}}{2a+4}$;
(2)原式=$\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}$=$\sqrt{2}$+1;
(3)原式=$\frac{(3\sqrt{5}-2\sqrt{3})^{2}}{(3\sqrt{5}+2\sqrt{3})(3\sqrt{5}-2\sqrt{3})}$=$\frac{45+12-12\sqrt{15}}{33}$=$\frac{57-12\sqrt{15}}{33}$.
点评 此题考查了分母有理化,正确找出分母的有理化因式是解本题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
10.若a、b、c是三个有理数.若a×b×c是正数,则( )
| A. | a、b、c同号 | B. | a是负数,b、c异号 | C. | b是负数,a、c同号 | D. | c是正数,a、b异号 |
 如图,已知AB∥DE∥CF,若∠ABC=70°,∠BCD=20°,求∠CDE的度数.
如图,已知AB∥DE∥CF,若∠ABC=70°,∠BCD=20°,求∠CDE的度数.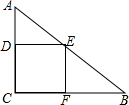 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少?
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少?