题目内容
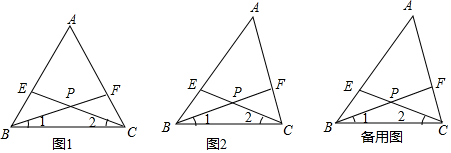
11.如图,将直角的顶点P放在正方形ABCD的对角线AC上,使角的一边交边BC于点E,另一边交射线DC于点F,过点P作直线MN∥AD,MN交AB于点M,交CD于点N.(1)证明:PE=PF;(只要证明图1这种情形)
(2)如图2,当点F在射线NC上时,探究线段DN,NF,BE之间有何等量关系,并加以证明;
(3)如图3,若将题中的正方形变为矩形ABCD,且AD=mCD,其余条件不变,探究线段DN,NF,BE之间的等量关系,利用图3和备用图画出图形,并直接写出相应的等量关系,不必证明.

分析 (1)利用同角的余角判断出∠EPQ=∠FPN,即可判断出△PQE≌△PNF(ASA),即可得出结论;
(2)先判断出DN=NF,同(1)的方法判断出△PQE≌△PNF(ASA),代换即可得出结论;
(3)分两种情况,类似(2)的方法利用相似即可得出结论.
解答 解:(1)如图1, 过点P作PQ⊥BC于Q,
过点P作PQ⊥BC于Q,
∴四边形CNPQ是正方形,
∴PN=PQ=CN,∠NPF+∠FPQ=90°,
∵∠EPQ+∠FPQ=90°,
∴∠EPQ=∠FPN,
在△PQE和△PNF中,$\left\{\begin{array}{l}{∠PQE=∠PNF}\\{PQ=PN}\\{∠EPQ=∠FPN}\end{array}\right.$,
∴△PQE≌△PNF(ASA),
∴PE=PF,
(2)DN=BE+NF,理由:如图2,
过点P作PQ⊥BC于Q,
同(1)的方法得,四边形CNPQ是正方形,
∴CN=CQ,
∵BC=DC,
∴DN=BQ,
同(1)的方法得,△PQE≌△PNF(ASA),
∴EQ=NF,
∴DN=BQ=BE+EQ=BE+NF;
(3)①当点F在边CD上时,如图3,
∵MN∥AD,
∴∠PNC=90°,
∴tan∠ACD=$\frac{AD}{CD}=\frac{PN}{CN}$,
∵AD=mCD,
∴PN=mCN,
过点P作PQ⊥BC于Q,
∴四边形CNPQ是矩形,
∴PQ=CN,
∴PN=mPQ,
同理:BQ=PM=mAM=mDN,
同(1)的方法得,∠EPQ=∠FPN,
∵∠PQE=∠PNF,
∴△PQE∽△PNF,
∴$\frac{EQ}{NF}=\frac{PQ}{PN}$,
∴NF=mEQ,
∴NF=m(BQ-BE)=mBQ-mBE=m•mDN-mBE,
∴NF+mBE=m2DN,
②当点F在DC的延长线时,如图4,
同①的方法得出:NF+mBE=m2DN.
点评 此题是相似形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,正方形的判定和性质,矩形的判定和性质,解(1)(2)的关键是构造全等三角形,解(3)的关键是构造相似三角形,是一道典型的中考常考题.

 名校课堂系列答案
名校课堂系列答案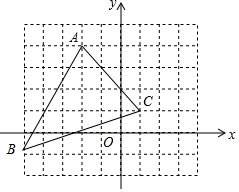 如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )| A. | (3,1) | B. | (9,-4) | C. | (-6,7) | D. | (-1,2) |
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (-2,1) |
| A. | $\left\{\begin{array}{l}a+b=1\\ 2a+b=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}3a+b=3\\ 2a+b=4\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}a+b=1\\ 3a-2c=19\end{array}\right.$ | D. | $\left\{\begin{array}{l}5a-2b=19\\ 3a+b=3\end{array}\right.$ |
 如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.