Question

6．如图，△ABC中，点E、F分别在边AB，AC上，BF与CE相交于点P，且∠1=∠2=$\frac{1}{2}$∠A．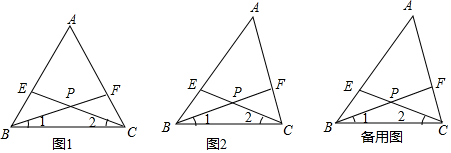

（1）如图1，若AB=AC，求证：BE=CF；
（2）若图2，若AB≠AC，
①（1）中的结论是否成立？请给出你的判断并说明理由；
②求证：$\frac{BF}{CE}$=$\frac{AB}{AC}$．

Answer 1

分析 （1）由等腰三角形的性质得到∠EBC=∠FCB，根据全等三角形的判定和性质即可得到结论；
（2）①作∠A的平分线交BC于点D，连结DE、DF，于是得到∠DAF=∠DAE=$\frac{1}{2}$∠A，根据已知条件得到∠DAF=∠DAE=∠1=∠2，推出A、B、D、F四点与A、E、D、C四点分别共圆，于是得到BD=DF，DE=DC，根据全等三角形的性质即可得到结论；②根据相似三角形的性质得到$\frac{BF}{CE}=\frac{BD}{DC}$，根据三角形角平分线定理得到$\frac{AB}{AC}=\frac{BD}{DC}$，等量代换即可得到结论．

解答 解：（1）∵AB=AC，
∴∠EBC=∠FCB，
在△BCE与△CBF中，$\left\{\begin{array}{l}{∠EBC=∠FCB}\\{BC=CB}\\{∠1=∠2}\end{array}\right.$，
∴△BCE≌△CBF，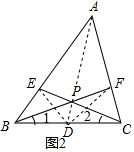
∴BE=CF；
（2）①成立，理由如下：作∠A的平分线交BC于点D，连结DE、DF，
则∠DAF=∠DAE=$\frac{1}{2}$∠A，
∵∠1=∠2=$\frac{1}{2}$∠A，
∴∠DAF=∠DAE=∠1=∠2，
∴A、B、D、F四点与A、E、D、C四点分别共圆，
∴BD=DF，DE=DC，
∵∠BDE=∠A，∠CDF=∠A，
∴∠BDE=∠CDF，
在△DEB与△DCF中，$\left\{\begin{array}{l}{BD=DF}\\{∠BDE=∠CDF}\\{DE=DC}\end{array}\right.$，
∴△DEB≌△DCF，
∴BE=CF；
②由上面的证明易知△DFB与△DEC均为等腰三角形，
∵∠1=∠2，
∴△DFB∽△DEC，
∴$\frac{BF}{CE}=\frac{BD}{DC}$，
∵AD是△ABC的内角平分线，
∴$\frac{AB}{AC}=\frac{BD}{DC}$，
∴$\frac{BF}{CE}=\frac{AB}{AC}$．

点评 本题考查了相似三角形的判定和性质，全等三角形的判定和性质，等腰三角形的判定和性质，三角形角平分线定理，正确的作出辅助线是解题的关键．