题目内容
2.计算:(x+1)(x-1)=x2-1.(-x+3)2=x2-6x+9.分析 依据平方差公式和完全平方公式进行计算即可.
解答 解::(x+1)(x-1)=x2-1;
(-x+3)2=x2-6x+9.
故答案为:x2-1;x2-6x+9.
点评 本题主要考查的是平方差公式和完全平方公式的应用,熟练掌握平方差公式和完全平方公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=4 | C. | 5$\sqrt{3}$-$\sqrt{27}$=2$\sqrt{3}$ | D. | $\sqrt{{x}^{2}}$=x |
10. 如图,△ABC沿BC边所在的直线向右平移得到△DEF,下列结论中错误的是( )
如图,△ABC沿BC边所在的直线向右平移得到△DEF,下列结论中错误的是( )
 如图,△ABC沿BC边所在的直线向右平移得到△DEF,下列结论中错误的是( )
如图,△ABC沿BC边所在的直线向右平移得到△DEF,下列结论中错误的是( )| A. | AC∥DF | B. | ∠A=∠D | C. | AC=DF | D. | EC=CF |
14.方程组$\left\{{\begin{array}{l}{x-y=1}\\{2x+y=5}\end{array}}\right.$的解是( )
| A. | $\left\{{\begin{array}{l}{x=2}\\{y=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=-1}\\{y=2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=-2}\\{y=-1}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=2}\\{y=-1}\end{array}}\right.$ |
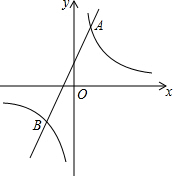 已知反比例函数y=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).