题目内容
1.已知:线段a及∠ACB.求作:⊙O,使⊙O在∠ACB的内部,CO=a,且⊙O与∠ACB的两边分别相切.

分析 首先作出∠ACB的平分线CD,再截取CO=a得出圆心O,作OE⊥CA,由角平分线的性质和切线的判定作出圆即可.
解答 解:①作∠ACB的平分线CD,
②在CD上截取CO=a,
③作OE⊥CA于E,以O为圆心,OE长为半径作圆;
如图所示:⊙O即为所求.
点评 本题考查了作图-复杂作图、角平分线的性质、切线的判定;熟练掌握角平分线的作图,找出圆心O是解决问题的关键.

练习册系列答案
相关题目
11.(1)计算:($\frac{1}{3}$)-2-|1-$\sqrt{2}$|+(π-3.14)0+$\frac{1}{2}$$\sqrt{8}$+tan60°
(2)解方程:2x2-3x-3=0.
(2)解方程:2x2-3x-3=0.
9.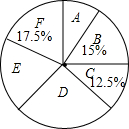 某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
根据图表提供的信息,下列结论错误的是( )
 某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)| 选修课 | A | B | C | D | E | F |
| 人数 | 40 | 60 | 100 |
| A. | 这次被调查的学生人数为400人 | |
| B. | 扇形统计图中E部分扇形的圆心角为72° | |
| C. | 被调查的学生中喜欢选修课E、F的人数分别为80,70 | |
| D. | 喜欢选修课C的人数最少 |
16.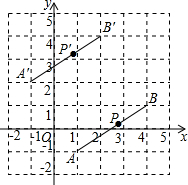 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )| A. | (a-2,b+3) | B. | (a-2,b-3) | C. | (a+2,b+3) | D. | (a+2,b-3) |
6. 如图,l1∥l2,∠1=56°,则∠2的度数为( )
如图,l1∥l2,∠1=56°,则∠2的度数为( )
 如图,l1∥l2,∠1=56°,则∠2的度数为( )
如图,l1∥l2,∠1=56°,则∠2的度数为( )| A. | 34° | B. | 56° | C. | 124° | D. | 146° |
11.若x1,x2是一元二次方程x2-2x-1=0的两个根,则x12-x1+x2的值为( )
| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
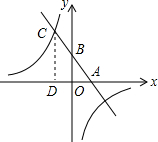 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6. 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$.
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$.