题目内容
7. 2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 首先过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,易得四边形ABFE为矩形,根据矩形的性质,可得AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=3500米,然后分别在Rt△AEC与Rt△BFD中,利用三角函数即可求得CE与DF的长,继而求得岛屿两端A、B的距离.
解答 解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=300米,CD=3500米.
在Rt△AEC中,∠C=60°,AE=300米.
∴CE=$\frac{AE}{tan60°}$=$\frac{300}{\sqrt{3}}$=100$\sqrt{3}$(米),
在Rt△BFD中,∠BDF=45°,BF=300.
∴DF=BF=300(米).
∴AB=EF=CD+DF-CE=3500+300-100$\sqrt{3}$≈3800-100×1.73≈3627(米),
答:岛屿两端A、B的距离为3627米.
点评 此题考查了俯角的定义、解直角三角形与矩形的性质.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
18.如果一个实数的算术平方根等于它的立方根,那么满足条件的实数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 定义:将一个图形L沿某个方向平移一段距离后,该图形在平面上留下的痕迹称之为图形L在该方向的拖影.如图,四边形ABB′A′是线段AB水平向右平移得到的拖影.则将下面四个图形水平向右平移适当距离,其拖影是五边形的是( )
定义:将一个图形L沿某个方向平移一段距离后,该图形在平面上留下的痕迹称之为图形L在该方向的拖影.如图,四边形ABB′A′是线段AB水平向右平移得到的拖影.则将下面四个图形水平向右平移适当距离,其拖影是五边形的是( )



 如下图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为3.75.
如下图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为3.75.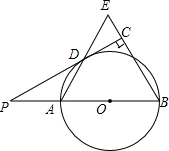 如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.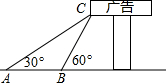 如图,某校数学兴趣小组为了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到点B处,又测得C点的仰角为60°.请你根据以上数据求C点离地面的高度(结果保留根号).
如图,某校数学兴趣小组为了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到点B处,又测得C点的仰角为60°.请你根据以上数据求C点离地面的高度(结果保留根号).