题目内容
15.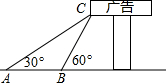 如图,某校数学兴趣小组为了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到点B处,又测得C点的仰角为60°.请你根据以上数据求C点离地面的高度(结果保留根号).
如图,某校数学兴趣小组为了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到点B处,又测得C点的仰角为60°.请你根据以上数据求C点离地面的高度(结果保留根号).
分析 根据题意作出合适的辅助线,表示出30°角和60°角的正切值,根据它们的对边都是BD可以建立关系,得到AD和BD的长,从而可以得到CD的长,本题得以解决.
解答 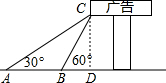 解:作CD⊥AB交AB的延长线于点D,如右图所示,
解:作CD⊥AB交AB的延长线于点D,如右图所示,
∵tan30°=$\frac{CD}{AD}$,tan60°=$\frac{CD}{BD}$,
∴tan30°•AD=tan60°•BD,
即$\frac{\sqrt{3}}{3}AD=\sqrt{3}BD$,
∴AD=3BD,
又∵AD=10+BD,
∴AD=15,BD=5,
∴CD=tan60°•BD=$\sqrt{3}×5=5\sqrt{3}$m,
即C点离地面的高度是$5\sqrt{3}$m.
点评 本题考查解直角三角形的应用-仰角俯角问题,解题的关键是明确题意,找出题目中的等量关系,利用特殊角的三角函数值解答问题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
6.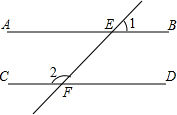 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )| A. | 44° | B. | 46° | C. | 134° | D. | 144° |
 2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)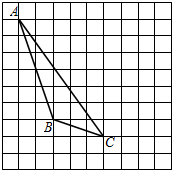 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图.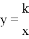 上,AB丄x轴于B,且△AOB的面积S△AOB=2,则k=__________.
上,AB丄x轴于B,且△AOB的面积S△AOB=2,则k=__________.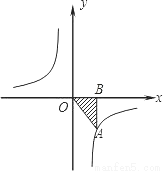
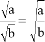 后,认为
后,认为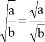 也成立,因此他认为一个化简过程:
也成立,因此他认为一个化简过程: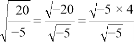
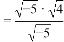 =
=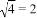 是正确的.你认为他的化简对吗?如果不对,请说明理由并改正.
是正确的.你认为他的化简对吗?如果不对,请说明理由并改正.