题目内容
19.观察下列算式:$\frac{1}{6}=\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$、$\frac{1}{12}=\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$、$\frac{1}{20}=\frac{1}{4×5}=\frac{1}{4}-\frac{1}{5}…$
(1)由此可推断:$\frac{1}{42}$=$\frac{1}{6}$-$\frac{1}{7}$;
(2)请用含字母m(m为正整数)的等式表示(1)中的一般规律$\frac{1}{m(m+1)}$=$\frac{1}{m}$-$\frac{1}{m+1}$;;
(3)仿照以上方法可推断:$\frac{2}{35}$=$\frac{1}{5}$-$\frac{1}{7}$;
(4)仿照以上方法解方程:$\frac{3}{(x-1)(x-4)}=\frac{1}{x-1}$.
分析 (1)根据已知等式得出规律,计算即可得到结果;
(2)写出一般性规律即可;
(3)仿照以上方法将原式变形即可;
(4)方程变形后,计算即可求出解.
解答 解:(1)$\frac{1}{42}$=$\frac{1}{6×7}$=$\frac{1}{6}$-$\frac{1}{7}$;
(2)$\frac{1}{m(m+1)}$=$\frac{1}{m}$-$\frac{1}{m+1}$;
(3)$\frac{2}{35}$=$\frac{2}{5×7}$=$\frac{1}{5}$-$\frac{1}{7}$;
(4)方程整理得:$\frac{1}{x-4}$-$\frac{1}{x-1}$=$\frac{1}{x-1}$,即$\frac{1}{x-4}$=$\frac{2}{x-1}$,
去分母得:x-1=2x-8,
解得:x=7,
经检验x=7是分式方程的解.
故答案为:(1)$\frac{1}{6}$-$\frac{1}{7}$;(2)$\frac{1}{m(m+1)}$=$\frac{1}{m}$-$\frac{1}{m+1}$;(3)$\frac{1}{5}$-$\frac{1}{7}$;
点评 此题考查了解分式方程,弄清题中的拆项规律是解本题的关键.

练习册系列答案
相关题目
7.要使分式$\frac{x-3}{x-2}$有意义,那么x的取值范围是( )
| A. | x>2 | B. | x>3 | C. | x≠2 | D. | x≠3 |
6.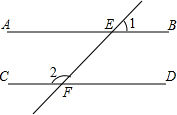 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )| A. | 44° | B. | 46° | C. | 134° | D. | 144° |
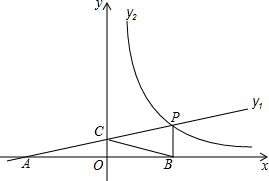 如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC.
如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC. 2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)