题目内容
15．解不等式组：$\left\{\begin{array}{l}{3x+1≥2x（1）}\\{2x-3≤5（2）}\end{array}\right.$，并把解集在数轴上表示出来．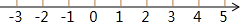
分析 分别求出两个不等式的解集，然后在数轴上表示出两个不等式解集的公共部分即可．
解答 解：解不等式（1），得x≥-1，
解不等式（2），得x≤4，
把不等式（1）和（2）的解集在数轴上表示出来，如图所示．
从上图可以找出两个不等式解集的公共部分，得不等式组的解集为：-1≤x≤4．
点评 本题考查了解一元一次不等式组：求解出两个不等式的解集，然后按照“同大取大，同小取小，大于小的小于大的取中间，小于小的大于大的无解”确定不等式组的解集．
练习册系列答案
相关题目
7．要使分式$\frac{x-3}{x-2}$有意义，那么x的取值范围是（ ）
| A． | x＞2 | B． | x＞3 | C． | x≠2 | D． | x≠3 |
20．分别写有0，2-1，-2，cos30°，3的五张卡片，除数不同外其他均相同，从中任意抽取一张，那么抽到负数的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习，在返回济州岛军事基地途中，韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了3500米，在点D测得这小岛的东端点B的俯角为45°，求这个济州小岛东西两端BA的距离（结果精确到1米，参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）
3．要使式子$\sqrt{3-m}$有意义，则x的取值范围是（ ）
| A． | m≤3 | B． | m＜3 | C． | m≥3 | D． | m＞3 |