题目内容
4.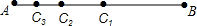 如图所示,AB=16cm,
如图所示,AB=16cm,(1)若C1是AB的中点,求AC1的长度;
(2)若C2是AC1的中点,求AC2的长度;
(3)若C3是AC2的中点,求AC3的长度;
(4)若照上述规律发展下去,则ACn的长度是多少呢?
分析 (1)根据线段中点的性质,可得AC1的长度;
(2)根据线段中点的性质,可得AC2的长度;
(3)根据线段中点的性质,可得AC3的长度;
(4)根据线段中点的性质,可得ACn的长度.
解答 解:(1)C1是AB的中点,AB=16cm,得
AC1=$\frac{1}{2}$AB=8cm,
AC1的长度为8cm;
(2)C2是AC1的中点,AC1=8cm,得
AC1=$\frac{1}{2}$AC1=$\frac{1}{2}$×$\frac{1}{2}$AB=($\frac{1}{2}$)2AB=4cm,
AC2的长度为4cm;
(3)C3是AC2的中点,AC2=4cm,得
AC3=$\frac{1}{2}$AC2=$\frac{1}{2}$×$\frac{1}{2}$AC1=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$AB=$\frac{1}{2}$×($\frac{1}{2}$)2AB=($\frac{1}{2}$)3AB=2cm,
AC3的长度为2cm;
(4)由以上规律,得
ACn=16×$(\frac{1}{2})$n,
ACn的长度是16×$(\frac{1}{2})$n.
点评 本题考查了两点间的距离,利用线段中点的性质得出规律:第n个中点分线段所得的线段是原线段的($\frac{1}{2}$)n是解题关键.

练习册系列答案
相关题目
15.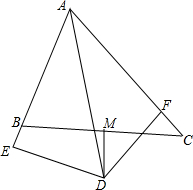 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE;其中正确的有( )
 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE;其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.下列命题是真命题的是( )
| A. | 同位角相等 | B. | 平行于同一直线的两条直线平行 | ||
| C. | 点(2,3)在直线y=2x+3上 | D. | 函数y=-x+1中y随x的增大而增大 |
 如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).
如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).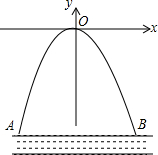 某涵洞是一条抛物线形,它的截面如图所示,现测得水面宽AB=10.6cm,涵洞顶点O到水面的距离为2.4cm,在图中的直角坐标系内,涵洞所在的抛物线的解析式为y=-$\frac{240}{2809}$x2.
某涵洞是一条抛物线形,它的截面如图所示,现测得水面宽AB=10.6cm,涵洞顶点O到水面的距离为2.4cm,在图中的直角坐标系内,涵洞所在的抛物线的解析式为y=-$\frac{240}{2809}$x2.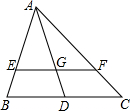 如图,△ABC中,EF∥BC,AD交EF于G.
如图,△ABC中,EF∥BC,AD交EF于G.