题目内容
15.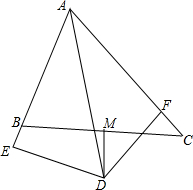 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE;其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由角平分线的性质可知①正确;②由题意可知∠EAD=∠FAD=30°,故此可知ED=$\frac{1}{2}AD$,DF=$\frac{1}{2}DF$,从而可证明②正确;③若DM平分∠ADF,则∠EDM=90°,从而得到∠ABC为直角三角形,条件不足,不能确定,故③错误;④连接BD、DC,然后证明△EBD≌△DFC,从而得到BE=FC,从而可证明④.
解答 解:如图所示:连接BD、DC.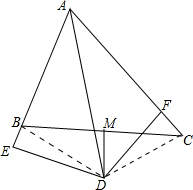
①∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴ED=DF.
∴①正确.
②∵∠EAC=60°,AD平分∠BAC,
∴∠EAD=∠FAD=30°.
∵DE⊥AB,
∴∠AED=90°.
∵∠AED=90°,∠EAD=30°,
∴ED=$\frac{1}{2}$AD.
同理:DF=$\frac{1}{2}AD$.
∴DE+DF=AD.
∴②正确.
③由题意可知:∠EDA=∠ADF=60°.
假设MD平分∠ADF,则∠ADM=30°.则∠EDM=90°,
又∵∠E=∠BMD=90°,
∴∠EBM=90°.
∴∠ABC=90°.
∵∠ABC是否等于90°不知道,
∴不能判定MD平分∠ADF.
故③错误.
④∵DM是BC的垂直平分线,
∴DB=DC.
在Rt△BED和Rt△CFD中$\left\{\begin{array}{l}{DE=DF}\\{BD=DC}\end{array}\right.$,
∴Rt△BED≌Rt△CFD.
∴BE=FC.
∴AB+AC=AE-BE+AF+FC
又∵AE=AF,BE=FC,
∴AB+AC=2AE.
故④正确.
故选:C.
点评 本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
5.下列语句正确的是( )
| A. | 画射线AB=10cm | B. | 射线AB和射线BA是同一条射线 | ||
| C. | 射线AB与射线AC可以是同一条射线 | D. | 延长射线AB |
3.我市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售,则平均每次下调的百分率是( )
| A. | 12% | B. | 30% | C. | 19% | D. | 10% |
20. 如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
 如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )| A. | 69 | B. | 54 | C. | 27 | D. | 40 |
7.下列几何图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 线段 | B. | 等边三角形 | C. | 平行四边形 | D. | 正五边形 |
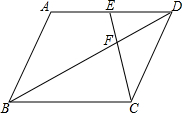 如图,在?ABCD中,F是对角线BD上的一点,连接CF并延长交AD于点E.若$\frac{BF}{DF}$=$\frac{1}{n}$,则$\frac{EF}{EC}$=n:(n+1).
如图,在?ABCD中,F是对角线BD上的一点,连接CF并延长交AD于点E.若$\frac{BF}{DF}$=$\frac{1}{n}$,则$\frac{EF}{EC}$=n:(n+1). 如图所示,AB=16cm,
如图所示,AB=16cm,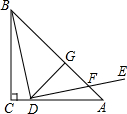 如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2$\sqrt{2}$,则△BDG的面积为96.
如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2$\sqrt{2}$,则△BDG的面积为96.