题目内容
12.计算:(1)用公式法解方程:x2+3x-2=0
(2)已知a2+a=0,请求出代数式($\frac{3}{{a}^{2}-9}+\frac{1}{a+3}$)$÷\frac{{a}^{2}}{a-3}$的值.
分析 (1)首先找出公式中的a,b,c的值,再代入求根公式求解即可.
(2)首先把括号内的分式进行通分,进行加法运算,然后把除法转化成乘法,进行乘法运算,然后把已知的式子求出a的值,代入化简以后的式子即可求解.
解答 解:(1)a=1,b=3,c=-2,
△=b2-4ac=9+8=17,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-3±\sqrt{17}}{2×1}$=$\frac{-3±\sqrt{17}}{2}$,
则:x1=$\frac{-3+\sqrt{17}}{2}$,x2=$\frac{-3-\sqrt{17}}{2}$
(2).解:原式=[$\frac{3}{(a+3)(a-3)}$+$\frac{a-3}{(a+3)(a-3)}$]÷$\frac{{a}^{2}}{a-3}$
=$\frac{a}{(a+3)(a-3)}$•$\frac{a-3}{{a}^{2}}$
=$\frac{1}{{a}^{2}+3a}$;
由a2+a=0,解得:a=0或-1,
当a=0时,原分式无意义,
当a=-1时,原式=$\frac{1}{1-3}$=-$\frac{1}{2}$.
点评 本题考查了分式的化简求值:先把分式的分子或分母因式分解,再进行通分或约分,得到最简分式或整式,然后把满足条件的字母的值代入计算得到对应的分式的值.由考查了公式法解一元二次方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.我市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售,则平均每次下调的百分率是( )
| A. | 12% | B. | 30% | C. | 19% | D. | 10% |
20. 如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
 如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )| A. | 69 | B. | 54 | C. | 27 | D. | 40 |
7.下列几何图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 线段 | B. | 等边三角形 | C. | 平行四边形 | D. | 正五边形 |
17.四位同学解方程$\frac{1}{2}$-$\frac{x-3}{3}$=1,下面是他们解方程中去分母的一步,其中正确的是 ( )
| A. | 1-(x-3)=1 | B. | 3-2(x-3)=6 | C. | 2-3(x-3)=6 | D. | 3-2(x-3)=1 |
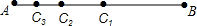 如图所示,AB=16cm,
如图所示,AB=16cm,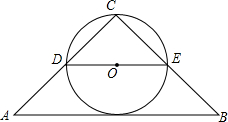 如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.
如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.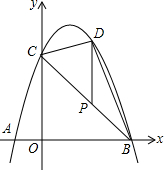 如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).
如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).