题目内容
13.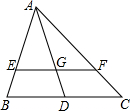 如图,△ABC中,EF∥BC,AD交EF于G.
如图,△ABC中,EF∥BC,AD交EF于G.(1)图中有几对相似三角形?是哪几对?
(2)$\frac{EG}{BD}$和$\frac{GF}{DC}$相等吗?为什么?
(3)若EG=2,GF=3,BD=5,求DC长.
分析 (1)根据平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似即可解答;
(2)根据EF∥BC,于是得到△AEG∽△ABD,△AGF∽△ADC,根据相似三角形的性质得到$\frac{EG}{BD}=\frac{AG}{AD}$,$\frac{GF}{CD}=\frac{AG}{AD}$,等量代换得到$\frac{EG}{BD}$=$\frac{GF}{DC}$;
(3)根据$\frac{EG}{BD}$=$\frac{GF}{DC}$,代入数据即可得到结论.
解答 解:(1)图中共有3对相似三角形,
理由如下:
∵EF∥BC,分别交AB,AC,AD于点E,F,G,
∴△AEG∽△ABD,△AGF∽△ADC,△AEF∽△ABC;
(2)$\frac{EG}{BD}$和$\frac{GF}{DC}$相等,
理由:∵EF∥BC,
∴△AEG∽△ABD,△AGF∽△ADC,
∴$\frac{EG}{BD}=\frac{AG}{AD}$,$\frac{GF}{CD}=\frac{AG}{AD}$,
∴$\frac{EG}{BD}$=$\frac{GF}{DC}$;
(3)∵$\frac{EG}{BD}$=$\frac{GF}{DC}$,EG=2,GF=3,BD=5,
∴$\frac{2}{5}=\frac{3}{CD}$,
CD=$\frac{15}{2}$.
点评 本题主要考查相似三角形的平行线判定法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A”型和“X”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形.

练习册系列答案
相关题目
 如图所示,AB=16cm,
如图所示,AB=16cm,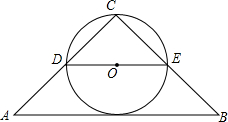 如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.
如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.
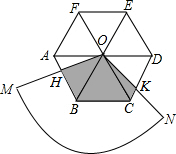 如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.
如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.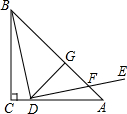 如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2$\sqrt{2}$,则△BDG的面积为96.
如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2$\sqrt{2}$,则△BDG的面积为96.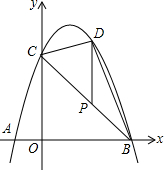 如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).
如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).