题目内容
13．下列四个几何体中，俯视图为正方形的是（ ）| A． |  球 | B． |  圆柱 | C． |  圆锥 | D． |  正方形 |
分析 分别利用几何体得出其俯视图的形状进而得出答案．
解答 解：A、其俯视图为圆，故此选项错误；
B、其俯视图为圆，故此选项错误；
C、其俯视图为圆，且有圆心，故此选项错误；
D、其俯视图为正方形，故此选项正确；
故选：D．
点评 此题主要考查了简单几何体的三视图，正确掌握俯视图的定义是解题关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
3．小军同学在学校组织的社会实践活动中，负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表：
（1）请根据题中已有的信息补全频数分布：①15，②6，③12%；
（2）如果家庭月均用水量在5≤x＜8范围内为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户？
（3）记月均用水量在2≤x＜3范围内的两户为a1，a2，在7≤x＜8范围内的3户b1、b2、b3，从这5户家庭中任意抽取2户，试完成下表，并求出抽取出的2户家庭来自不同范围的概率．
| 月均用水量 | 2≤x＜3 | 3≤x＜4 | 4≤x＜5 | 5≤x＜6 | 6≤x＜7 | 7≤x＜8 | 8≤x＜9 |
| 频数 | 2 | 12 | ① | 10 | ② | 3 | 2 |
| 百分比 | 4% | 24% | 30% | 20% | ③ | 6% | 4% |
（2）如果家庭月均用水量在5≤x＜8范围内为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户？
（3）记月均用水量在2≤x＜3范围内的两户为a1，a2，在7≤x＜8范围内的3户b1、b2、b3，从这5户家庭中任意抽取2户，试完成下表，并求出抽取出的2户家庭来自不同范围的概率．
| a1 | a2 | b1 | b2 | b3 | |
| a1 | |||||
| a2 | |||||
| b1 | |||||
| b2 | |||||
| b3 |
小明上学途中要经过A，B两地，由于A，B两地之间有一片草坪，所以需要走路线AC，CB，如图，在△ABC中，AB=63m，∠A=45°，∠B=37°，求AC，CB的长．（结果保留小数点后一位）
1．下列五个图形：
①等腰直角三角形；②正方形；③正五边形；④正八边形；⑤圆．
其中既是轴对称图形又是中心对称图形的有（ ）
①等腰直角三角形；②正方形；③正五边形；④正八边形；⑤圆．
其中既是轴对称图形又是中心对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．
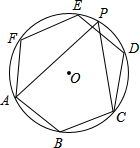如图，正六边形ABCDEF内接于⊙O，点P为$\widehat{DE}$上一点，则tan∠APC的值为（ ）
如图，正六边形ABCDEF内接于⊙O，点P为$\widehat{DE}$上一点，则tan∠APC的值为（ ）| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 1 |
18．计算（-2xy）2的结果是（ ）
| A． | 4x2y2 | B． | 4xy2 | C． | 2x2y2 | D． | 4x2y |
2．若a，b，c这三个数的平均数为2，方差为s2，则a+2，b+2，c+2的平均数和方差分别是（ ）
| A． | 2，s2 | B． | 4，s2 | C． | 2，s2+2 | D． | 4，s2+4 |
3．
在拼图游戏中，从图1的四张纸片中，任取两张纸片，能拼成“小房子”（如图2）的概率等于（ ）
在拼图游戏中，从图1的四张纸片中，任取两张纸片，能拼成“小房子”（如图2）的概率等于（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | 1 |