题目内容
8.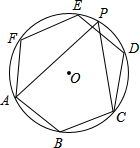 如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )
如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
分析 由正六边形的性质得出∠AOC=120°,由圆周角定理求出∠APC=60°,即可得出结果.
解答 解:连接OA、OB、OC,如图所示:
∵∠AOB=∠BOC=$\frac{360°}{6}$=60°,
∴∠AOC=120°,
∴∠APC=$\frac{1}{2}$∠AOC=60°,
∴tan∠APC=$\sqrt{3}$;
故选:A.
点评 本题考查了正六边形的性质、圆周角定理;熟练掌握正六边形的性质,由圆周角定理求出∠APC=60°是解决问题的关键.

练习册系列答案
相关题目
18.四个数-3,0,1,2,其中负数是( )
| A. | -3 | B. | 0 | C. | 1 | D. | 2 |
19. 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )| A. | 0.324πm2 | B. | 0.288πm2 | C. | 1.08πm2 | D. | 0.72πm2 |
16.若分式$\frac{x-2}{x+5}$的值为0,则x的值是( )
| A. | x=2 | B. | x=-2 | C. | x=-5 | D. | x=0 |
13.下列四个几何体中,俯视图为正方形的是( )
| A. |  球 | B. |  圆柱 | C. |  圆锥 | D. |  正方形 |
20.土家传统建筑的窗户上常有一些精致花纹、小辰对土家传统建筑非常感兴趣,他观察发现窗格的花纹排列呈现有一定规律,如图.其中“O”代表的就是精致的花纹,第1个图有5个花纹,第2个图有8个花纹,第3个图有11个花纹…,请问第7个图的精致花纹有( )


| A. | 26个 | B. | 23个 | C. | 20个 | D. | 17个 |
18.下列事件属于必然事件的是( )
| A. | 姚明罚球线上投篮,投进篮筐 | |
| B. | 某种彩票的中奖率为$\frac{1}{100}$,购买100张彩票一定中奖 | |
| C. | 掷一次骰子,向上一面的点数是6 | |
| D. | 367人中至少有两人的生日在同一天 |