题目内容
1.若4x2myn+1与-3x4y3的和是单项式,则m=2,n=2.分析 依据题意可知两个单项式为同类项,故此可列出关于m、n的方程,故此可求得m、n的值.
解答 解:∵4x2myn+1与-3x4y3的和是单项式,
∴2m=4,n+1=3.
解得:m=2,n=2.
故答案为:2;2.
点评 本题主要考查的是合并同类项,掌握同类项的定义是解题的关键.

练习册系列答案
相关题目
12.已知二次函数y1=a(x-2)2+k中,函数y1与自变量x的部分对应值如表:
(1)求该二次函数的表达式;
(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1)B(m+1,n2),试比较n1与n2的大小.
| x | … | 1 | 2 | 3 | 4 | … |
| y | … | 2 | 1 | 2 | 5 | … |
(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1)B(m+1,n2),试比较n1与n2的大小.
16.某电信公司给顾客提供了A、B、C三种宽带上网的收费方式:
设某用户每月的上网时间为x(小时),A、B、C三种收费方式的收费金额分别为y1、y2、y3(元).
(1)分别求y1、y1、y2关于x的函数关系式,并写出相应的自变量的取值范围;
(2)请你帮该用户选择较省钱的收费方式,并说明理由.
| 收费方式 | 月使用费/元 | 包时上网时间/小时 | 超时费/(元/分钟) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
(1)分别求y1、y1、y2关于x的函数关系式,并写出相应的自变量的取值范围;
(2)请你帮该用户选择较省钱的收费方式,并说明理由.
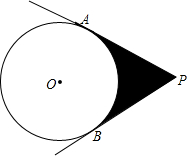 如图,PA,PB是⊙O的两条切线,切点分别为A,B,⊙O的半径为2cm,∠P=60°,求图中阴影部分的面积.
如图,PA,PB是⊙O的两条切线,切点分别为A,B,⊙O的半径为2cm,∠P=60°,求图中阴影部分的面积.
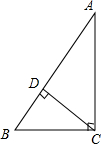 在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,D为垂足.求BD的长.
在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,D为垂足.求BD的长. 如图,已知AC交⊙O于点A、B,且BC等于圆的半径,连结OC交⊙O于点D,∠C=30°,求∠AOD的度数.
如图,已知AC交⊙O于点A、B,且BC等于圆的半径,连结OC交⊙O于点D,∠C=30°,求∠AOD的度数.