题目内容
2.当x=-2时,代数式$\frac{1-8{x}^{2}}{2}$的值是-$\frac{31}{2}$.分析 把x=-2代入代数式计算即可得到结果.
解答 解:当x=-2时,原式=$\frac{1-8×4}{2}$=-$\frac{31}{2}$,
故答案为:-$\frac{31}{2}$
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.把64开平方得( )
| A. | 8 | B. | -8 | C. | ±8 | D. | 32 |
13.小张同学说出了二次函数的两个条件:
(1)当x<1时,y随x的增大而增大;
(2)函数图象经过点(-2,4).
则符合条件的二次函数表达式可以是( )
(1)当x<1时,y随x的增大而增大;
(2)函数图象经过点(-2,4).
则符合条件的二次函数表达式可以是( )
| A. | y=-(x-1)2-5 | B. | y=2(x-1)2-14 | C. | y=-(x+1)2+5 | D. | y=-(x-2)2+20 |
10.一次函数y=kx+b,当-3≤x≤1时,对应的y的值为1≤y≤9,则kb的值为( )
| A. | 14 | B. | -6 | C. | -4或21 | D. | -6或14 |
17.已知△ABC中,tanA=$\frac{1}{2}$,下列说法正确的是( )
| A. | tanB=2 | B. | tanB=$\frac{1}{2}$ | C. | sinA=$\frac{2\sqrt{5}}{5}$ | D. | sinA=$\frac{\sqrt{5}}{5}$ |
12.已知二次函数y1=a(x-2)2+k中,函数y1与自变量x的部分对应值如表:
(1)求该二次函数的表达式;
(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1)B(m+1,n2),试比较n1与n2的大小.
| x | … | 1 | 2 | 3 | 4 | … |
| y | … | 2 | 1 | 2 | 5 | … |
(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1)B(m+1,n2),试比较n1与n2的大小.
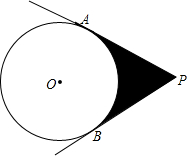 如图,PA,PB是⊙O的两条切线,切点分别为A,B,⊙O的半径为2cm,∠P=60°,求图中阴影部分的面积.
如图,PA,PB是⊙O的两条切线,切点分别为A,B,⊙O的半径为2cm,∠P=60°,求图中阴影部分的面积.