题目内容
16．
如图，△ABC中，∠C=90°，M是AB的中点，动点P从点A出发，沿AC方向匀速运动到终点C，动点Q从点C出发，沿CB方向匀速运动到终点B．已知P，Q两点同时出发，并同时到达终点，连接MP，MQ，PQ．在整个运动过程中，△MPQ的面积大小变化情况是（ ）| A． | 一直减小 | B． | 先减小后增大 | C． | 一直增大 | D． | 先增大后减小 |
分析 连接CM，根据点M是AB的中点可得△ACM和△BCM的面积相等，又P，Q两点同时出发，并同时到达终点，所以点P到达AC的中点时，点Q到达BC的中点，然后把开始时、结束时、与中点时的△MPQ的面积与△ABC的面积相比即可进行判断．
解答 
解：如图所示，连接CM，∵M是AB的中点，
∴S△ACM=S△BCM=$\frac{1}{2}$S△ABC，
开始时，S△MPQ=S△ACM=$\frac{1}{2}$S△ABC，
点P到达AC的中点时，点Q到达BC的中点时，S△MPQ=$\frac{1}{4}$S△ABC，
结束时，S△MPQ=S△BCM=$\frac{1}{2}$S△ABC，
所以，△MPQ的面积大小变化情况是：先减小后增大．
故选：B．
点评 本题考查了动点问题的函数图象，根据题意找出关键的开始时，中点时，结束时三个时间点的三角形的面积与△ABC的面积的关系是解题的关键．
练习册系列答案
相关题目
6．某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．设分配给甲店A型产品x件．两商店销售这两种产品每件的利润（元）如下表：
（1）分配给乙店B型产品x-10件（用含x的代数式表示）．
（2）设这家公司卖出这100件产品的总利润为W（元），求W关于x的函数关系式，并直接写出x的取值范围．
（3）若公司要求总利润不低于17560元，有几种不同分配方案？哪种方案总利润最大？请求出最大利润．
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
（2）设这家公司卖出这100件产品的总利润为W（元），求W关于x的函数关系式，并直接写出x的取值范围．
（3）若公司要求总利润不低于17560元，有几种不同分配方案？哪种方案总利润最大？请求出最大利润．
7．邻居王阿姨在再就业中心的扶持下，创办了“便民”报刊零售点，对经营的某种晚报，王阿姨提供了如下信息：
①买进报纸每份0.35元，卖出每份0.5元；
②一个月内（以30天计），有22天每天可以卖出250份，其余每天只能卖出150份；
③一个月内，每天从报社买进的报纸份数必须相同，当天卖剩下的报纸可以每份0.25元退回报社．
根据上述信息，请你给王阿姨帮个忙：
（1）填表：
（2）设每天从报社买进该晚报x份（150≤x≤250）时，月利润为y元，试求出y关于x的函数关系式，并求月利润的最大值．
①买进报纸每份0.35元，卖出每份0.5元；
②一个月内（以30天计），有22天每天可以卖出250份，其余每天只能卖出150份；
③一个月内，每天从报社买进的报纸份数必须相同，当天卖剩下的报纸可以每份0.25元退回报社．
根据上述信息，请你给王阿姨帮个忙：
（1）填表：
| 一个月内每天买进该晚报（份） | 150 | 200 |
| 当月利润（元） | 675 | 800 |
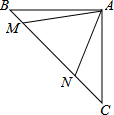如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°．若BM=1，CN=3，则MN的长为$\sqrt{10}$．
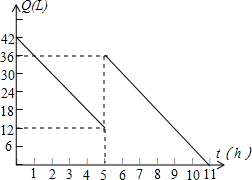机动车出发前油箱内有油42升，行驶若干小时后，途中在加油站若干升，油箱中余油量Q（升）与行驶时间t（时）之间的函数如图，根据图回答问题．
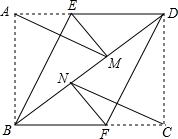在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．
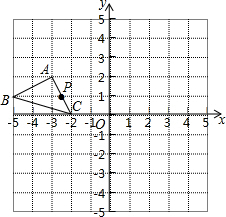如图，在10×10的正方形网格中，每个小正方形的边长均为1个单位．平面直角坐标系和△ABC的位置如图所示．
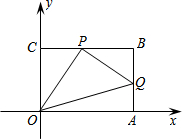已知：如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（6，0）、C（0，4），点P在BC边上运动，过P作PQ⊥OP，交AB边于Q，则AQ的最小值为$\frac{7}{4}$．