题目内容
11.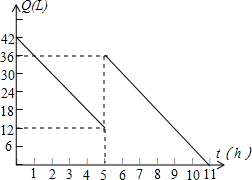 机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题.
机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题.(1)机动车行驶5 小时后加油;
(2)加油前油箱余油量Q与行驶时间t之间的函数关系式是42-6t,此函数自变量t的取值范围是0≤t≤5;
(3)中途加油24升;
(4)如果加油站距目的地还有230km,车速仍为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
分析 (1)图象上x=5时,对应着两个点,油量一多一少,可知此时加油了;
(2)因为x=0时,Q=42,x=5时,Q=12,所以出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,因此每小时耗油量为6L,由此即可写出函数解析式;
(3)因为x=5时,y有两个值12,36,所以加油(36-12)L;
(4)由图象知,加油后还可行驶6小时,即可行驶40×6千米,然后同230千米做比较,即可求出答案.
解答 解:(1)由图可得,机动车行驶5小时后加油;
(2)∵出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,
因此每小时耗油量为6L,
∴Q=42-6t(0≤t≤5);
(3)由图可得,36-12=24,
因此中途加油24L;
(4)由图可知,加油后可行驶6h,
故加油后行驶40×6=240km,
∵240>230,
∴油箱中的油够用.
故答案为:5;Q=42-6t,0≤t≤5;24.
点评 此题考查一次函数的实际应用,解答本题的关键是仔细观察图象,寻找题目中所给的信息,进而解决问题,难度一般.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
2. 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )| A. | 4$\sqrt{3}$π | B. | 4$\sqrt{2}$π | C. | 2$\sqrt{3}$π | D. | 4π |
16. 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直减小 | B. | 先减小后增大 | C. | 一直增大 | D. | 先增大后减小 |
 作图题(作图工具不限,保留作图痕迹,写出结论)
作图题(作图工具不限,保留作图痕迹,写出结论) (1)先化简,再求值:(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=$\frac{1}{3}$.
(1)先化简,再求值:(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=$\frac{1}{3}$.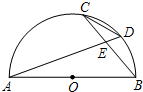 如图,AB是⊙O的直径,弦AD、BC相交于点E,若CD=5,AB=13,则sin∠BED=$\frac{12}{13}$.
如图,AB是⊙O的直径,弦AD、BC相交于点E,若CD=5,AB=13,则sin∠BED=$\frac{12}{13}$.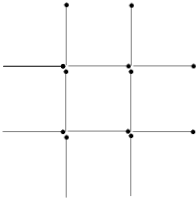 如图,12根火柴棒排成一个“井”字形,要求移动图中的4根火柴棒,使原图形变成三个相同的正方形,且没有火柴棒剩余(同一根火柴棒只能移动一次),你有什么好办法?试试看,画出移动后的图形,并标明移动前后的火柴棒.
如图,12根火柴棒排成一个“井”字形,要求移动图中的4根火柴棒,使原图形变成三个相同的正方形,且没有火柴棒剩余(同一根火柴棒只能移动一次),你有什么好办法?试试看,画出移动后的图形,并标明移动前后的火柴棒.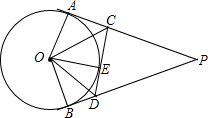 如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )
如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )