题目内容
5.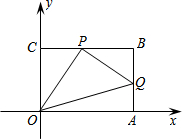 已知:如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(6,0)、C(0,4),点P在BC边上运动,过P作PQ⊥OP,交AB边于Q,则AQ的最小值为$\frac{7}{4}$.
已知:如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(6,0)、C(0,4),点P在BC边上运动,过P作PQ⊥OP,交AB边于Q,则AQ的最小值为$\frac{7}{4}$.
分析 设CP为x,BQ为y,证明△OCP∽△PBQ,根据相似三角形的性质,列出比例式,由含x的代数式表示y,求出y的最大值,得到AQ的最小值.
解答 解:设CP为x,BQ为y,
则PB=6-x,
∵四边形OABC是矩形,PQ⊥OP,
∴△OCP∽△PBQ,
∴$\frac{PC}{BQ}$=$\frac{OC}{PB}$,
∴y=-$\frac{1}{4}$x2+$\frac{3}{2}$x=-$\frac{1}{4}$(x-3)2+$\frac{9}{4}$,
y的最大值为:$\frac{9}{4}$,
∴AQ的最小值为:4-$\frac{9}{4}$=$\frac{7}{4}$,
故答案为:$\frac{7}{4}$.
点评 本题考查的二次函数的最值问题,证明三角形相似,根据相似三角形的性质,得到二次函数,根据二次函数的性质求出最值是解题的关键.

练习册系列答案
相关题目
16. 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直减小 | B. | 先减小后增大 | C. | 一直增大 | D. | 先增大后减小 |
13.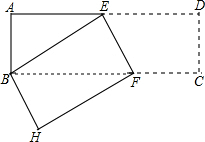 如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )
如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )
 如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )
如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )| A. | 27cm2 | B. | 24cm2 | C. | 22cm2 | D. | 20cm2 |
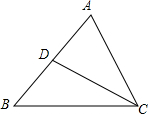 如图,已知CD是△ABC的中线,画出以点D为对称中心,与△ADC成中心对称的三角形.
如图,已知CD是△ABC的中线,画出以点D为对称中心,与△ADC成中心对称的三角形.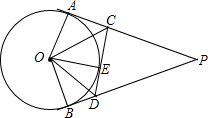 如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )
如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )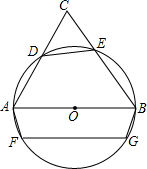 已知,如图,以△ABC的边AB作直径的⊙O,分别交AC、BC于点D、E,弦FG∥AB,S△CDE:S△ABC=1:4,DE=5cm,FG=8cm,求梯形AFGB的面积.
已知,如图,以△ABC的边AB作直径的⊙O,分别交AC、BC于点D、E,弦FG∥AB,S△CDE:S△ABC=1:4,DE=5cm,FG=8cm,求梯形AFGB的面积.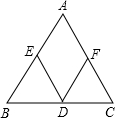 如图,在△ABC中,DE∥AC,DF∥AB.
如图,在△ABC中,DE∥AC,DF∥AB.