题目内容

7．在$\root{3}{9}$，$\sqrt{8}$，$\frac{22}{7}$，0.8888…，3π，0.262662666266662…，六个数中，无理数有4个．

分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．

解答 解：无理数有：$\root{3}{9}$，$\sqrt{8}$，3π，0.262662666266662…共4个．
故答案是：4．

点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．

练习册系列答案
相关题目
11．解下列方程
（1）7x+$\frac{1}{4}$=9x-$\frac{3}{2}$．
（2）$\frac{3x+1}{2}$=2-$\frac{2x+3}{5}$．
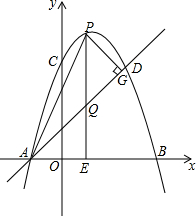18．如图，抛物线y=-x2+bx+c 经过A（-1，0），C（0，3）两点，点B是抛物线与x轴的另一个交点，点D与点C关于抛物线对称轴对称，作直线AD．点P在抛物线上，过点P作PE⊥x轴，垂足为点E，交直线AD于点Q，过点P作PG⊥AD，垂足为点G，连接AP．设点P的横坐标为m，PQ的长度为d．
（1）求抛物线的解析式；
（2）求点D的坐标及直线AD的解析式；
（3）当点P在直线AD上方时，求d关于m的函数关系式，并求出d的最大值；
（4）当点P在直线AD上方时，若PQ将△APG分成面积相等的两部分，直接写出m的值．
15．如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，水面下降1.5m时，水面宽度增加多少？
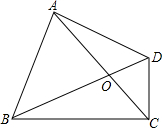2．四边形ABCD中，AC、BD相交于点O，∠BAD=90°且AB=AD，CD⊥BC，∠ACB=45°，AC=BC．
（1）求证：△DCA≌△OCB；
（2）若AC=4，求出四边形ABCD的面积．
12．将$1，-\frac{1}{2}，\frac{1}{3}，-\frac{1}{4}，\frac{1}{5}，-\frac{1}{6}，…$，按一定的规律排列如下：

请你写出第20行从左至右第10个数是（　　）
A．-$\frac{1}{198}$B．-$\frac{1}{200}$C．$\frac{1}{200}$D．$\frac{1}{202}$
19．比较大小：（填“＞”、“＜”或“=”）
2$\sqrt{7}$＞5； $\frac{\sqrt{3}-1}{2}$＜$\frac{1}{2}$；-3.14＞-π．
16．五张写着不同数字的卡片：-3，-1，0，+2，+4，请按要求抽出卡片，并完成下列各题：
（1）从中抽出2张卡片，使这2张卡片上的数字相除的商最小，如何抽取，最小值是多少？
（2）从中抽出3张卡片，使这3张卡片上的数字乘积最大，如何抽取？最大值是多少？
17．下列各式中，运算正确的是（　　）
A．$\sqrt{16}$=±4B．-|-9|=9C．（x3）2=x6D．$\sqrt{（2-x）^{2}}$=2-π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网