��Ŀ����
6�������Ǽס�����λͬѧ����������Ľ�����ж�����˵��������ɣ���ͬѧ����xȡ��ֵʱ����ʽ$\frac{{x}^{2}-1}{��x-1����x+2��}$��ֵΪ�㣿
�⣺������x2-1=0ʱ����x=��1ʱ����ʽ$\frac{{x}^{2}-1}{��x-1����x+2��}$��ֵΪ�㣮
��ͬѧ������ʽ$\frac{1}{1-\frac{1}{|x|}}$�����壬��x��ȡֵ��Χ��
�⣺��|x|��0����x��0ʱ����ʽ�����壬����x��ȡֵ��Χ��x��0��
���� ����ʽ��ֵΪ�㣬����ӵ����㣬�ҷ�ĸ�������㣬�ݴ˽��з��������
��� �⣺�ס�����ͬѧ�Ľ����ȷ���������£�
��ͬѧ��������x2-1=0���ң�x-1����x+2����0ʱ��$\frac{{x}^{2}-1}{��x-1����x+2��}$=0��
��x=-1ʱ����ʽ$\frac{{x}^{2}-1}{��x-1����x+2��}$��ֵΪ�㣮
��ͬѧ����|x|��0����|x|��1ʱ����ʽ$\frac{1}{1-\frac{1}{|x|}}$�����壬��x��0����x�١�1ʱ����ʽ$\frac{1}{1-\frac{1}{|x|}}$�����壮
���� ���⿼���˷�ʽ��ֵΪ��������ͷ�ʽ�����������������ʽ��ֵΪ�㣬��ͬʱ�߱�������������1������Ϊ0����2����ĸ��Ϊ0������������ȱһ���ɣ�

��ϰ��ϵ�д�
�����Ŀ
1��ij�¸�ְ������һ���㽶������ó�г����ۣ���֪�������㽶����x�����۶�y�Ĺ�ϵ�����ʾ��
��y��x�ĺ�����ϵʽ����ָ��y�Dz���x��һ�κ�����
| ����x��ǧ�ˣ� | 1 | 2 | 3 | 4 | 5 |
| ���۶�y��Ԫ�� | 4+0.1 | 8+0.2 | 12+0.3 | 16+0.4 | 20+0.5 |
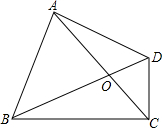 �ı���ABCD�У�AC��BD�ཻ�ڵ�O����BAD=90����AB=AD��CD��BC����ACB=45�㣬AC=BC��
�ı���ABCD�У�AC��BD�ཻ�ڵ�O����BAD=90����AB=AD��CD��BC����ACB=45�㣬AC=BC��