题目内容
19.王老师给同学们布置了这样一道习题:一个数的算术平方根为2m-6,它的平方根为±(m-2),求这个数.小张的解法如下:依题意可知,2m-6是m-2或者是-(m-2)两数中的一个…(1)
当2m-6=m-2,解得m=4…(2)
(2m-6)=(2×4-6)=2…(3)
这个数为4
当2m-6=-(m-2)时,解得m=$\frac{8}{3}$…(4)
(2m-6)=(2×$\frac{8}{3}$-6)=-$\frac{2}{3}$…(5)
这个数为$\frac{4}{9}$
综上可得,这个数为4或$\frac{4}{9}$…(6)
王老师看后说,小张的解法是错误的.你知道小张错在哪里吗?为什么?请予改正.
分析 由算术平方根的非负性质可知2m-6≥0,从而可对求得的m的值作出取舍.
解答 解:∵2m-6是某数的算术平方根,
∴2m-6≥0.
解得:m≥3.
∴当m=$\frac{8}{3}$不符合题意应舍去.
故答案为:这个数为4.
点评 本题主要考查的是算术平方根、平方根的定义,掌握算术平方根的非负性是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
10.要使分式$\frac{2x-3}{x+2}$有意义,则x的取值应满足( )
| A. | x=-2 | B. | x≠$\frac{3}{2}$ | C. | x>-2 | D. | x≠-2 |
4.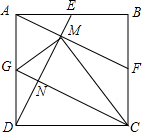 如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
①AF⊥DE;
②AF∥CG;
③CD=CM;
④∠CMD=∠AGM.
其中正确的有( )
 如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:①AF⊥DE;
②AF∥CG;
③CD=CM;
④∠CMD=∠AGM.
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
9.已知一个三角形的两边长分别为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长为( )
| A. | 13 | B. | 11 | C. | 13或11 | D. | 15 |
 如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.