题目内容
14.已知m+2n=2,关于整式①m2+4n(m+n),②2n2+mn+m的值,下列说法正确的是( )| A. | ①是常数,②不是常数 | B. | ①是不常数,②是常数 | ||
| C. | ①、②都是常数 | D. | ①、②都不是常数 |
分析 由已知条件得出m2+4n(m+n)=(m+2n)2=4,2n2+mn+m=n(2n+m)+m=2n+m=2,即可得出结论.
解答 解:∵m+2n=2,
∴m2+4n(m+n)=m2+4nm+4n2=(m+2n)2=22=4,
2n2+mn+m=n(2n+m)+m=2n+m=2,
∴①、②都是常数;
故选C.
点评 本题考查了完全平方公式、因式分解的方法;熟练掌握完全平方公式和提取公因式法分解因式是解决问题的关键.

练习册系列答案
相关题目
4.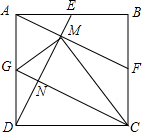 如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
①AF⊥DE;
②AF∥CG;
③CD=CM;
④∠CMD=∠AGM.
其中正确的有( )
 如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:①AF⊥DE;
②AF∥CG;
③CD=CM;
④∠CMD=∠AGM.
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
9.已知一个三角形的两边长分别为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长为( )
| A. | 13 | B. | 11 | C. | 13或11 | D. | 15 |
19. 如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )
如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )
 如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )
如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )| A. | $\sqrt{6}$:2 | B. | 3:2 | C. | $\sqrt{5}$:3 | D. | 5:3 |
16.下列式子正确的是( )
| A. | 5$<\sqrt{5}$ | B. | -$\sqrt{5}$$>-\sqrt{3}$ | C. | $\sqrt{5}-3$$<3-\sqrt{5}$ | D. | 0$<\sqrt{5}-3$ |

 给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.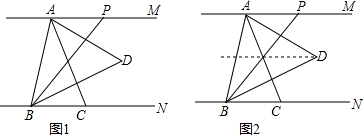
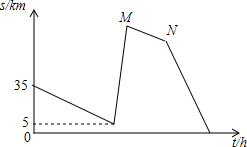 甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题:
甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题: