题目内容
4.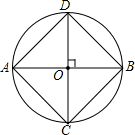 如图,AB、CD是⊙O的两条互相垂直的直径.
如图,AB、CD是⊙O的两条互相垂直的直径.(1)试判断四边形ACBD是什么特殊四边形,并说明理由;
(2)若四边形ACBD的面积为16,试求⊙O的面积.
分析 (1)由AC,BD是⊙O的两条直径,根据直径所对的圆周角是直角,即可得∠BAD=∠ABC=∠BCD=90°,则可判定四边形ABCD是矩形,然后根据线段垂直平分线的性质求得AC=AD,则可判定四边形ABCD是正方形;
(2)根据正方形的面积=$\frac{1}{2}$对角线的积求得半径,然后根据圆的面积公式求得即可.
解答 解:(1)四边形ABCD是正方形.
理由:∵AC,BD是⊙O的两条直径,
∴∠BAD=∠ABC=∠BCD=90°,
∴四边形ABCD是矩形,
∵AB垂直平分CD,
∴AC=AD,
∴四边形ABCD是正方形;
(2)∵S正方形=$\frac{1}{2}$AB•CD,AB=CD,
∴$\frac{1}{2}$AB2=16,
∴AB=4$\sqrt{2}$,
∴⊙O的半径为2$\sqrt{2}$,
∴S圆=πR2=8π.
点评 本题考查了圆周角定理,正方形的判定和性质,线段的垂直平分线的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
14.解方程:
(1)$\frac{x}{x-2}-\frac{2}{{x}^{2}-4}=1$
(2)$\frac{3}{x}-\frac{2}{1-x}=\frac{x+5}{{x}^{2}-x}$.
(1)$\frac{x}{x-2}-\frac{2}{{x}^{2}-4}=1$
(2)$\frac{3}{x}-\frac{2}{1-x}=\frac{x+5}{{x}^{2}-x}$.
15.一元二次方程x2+6x+9=0的解是( )
| A. | x=3 | B. | x1=3,x2=-3 | C. | x1=x2=-3 | D. | x1=x2=3 |
 如图,点A、B、C、D为⊙O上的一点,若∠A=40°,求∠OCB的度数.
如图,点A、B、C、D为⊙O上的一点,若∠A=40°,求∠OCB的度数.