题目内容
16.已知多项式(2x2+ax-y+6)-(2bx2-3x+5y-1).(1)若多项式的值与字母x的取值无关.求a、b的值;
(2)在(1)的条件下,先化简多项式3(a2-ab+b2)-($\frac{1}{2}$a2+ab+4b2),再求它的值.
分析 (1)先去括号得2x2+ax-y+6-2bx2+3x-5y+1合并得到(2-2b)x2+(a+3)x-6y+7,由于代数式的值与字母x的取值无关,则2-2b=0,a+3=0,解得a=-3,b=1;
(2)先去括号,合并化简后,代入a、b的数值得出答案即可.
解答 解:(1)原式=2x2+ax-y+6-2bx2+3x-5y+1=(2-2b)x2+(a+3)x-6y+7,
∵代数(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,
∴2-2b=0,a+3=0,
∴a=-3,b=1;
(2)3(a2-ab+b2)-($\frac{1}{2}$a2+ab+4b2)
=3a2-3ab+3b2-$\frac{1}{2}$a2-ab-4b2
=$\frac{5}{2}$a2-4ab-b2,
当a=-3,b=1时,
原式=$\frac{5}{2}$×9+12-1=$\frac{67}{2}$.
点评 此题考查整式的加减,代数式求值,掌握去括号法则和合并同类项的方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.(x2+y2)2-4(x2+y2)-5=0,则x2+y2的值为( )
| A. | 5 | B. | -1 | C. | 5或-1 | D. | 无法确定 |
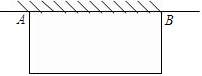 如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?
如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?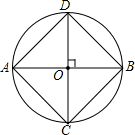 如图,AB、CD是⊙O的两条互相垂直的直径.
如图,AB、CD是⊙O的两条互相垂直的直径.