题目内容
18．若点A（-1，2），B（2，-3）在直线y=kx+b上，则函数y=$\frac{k}{x}$的图象在（ ）| A． | 第一、三象限 | B． | 第一、二象限 | C． | 第二、四象限 | D． | 第二、三象限 |
分析 待定系数法求得k、b的值，根据反比例函数的图象与性质即可判断．
解答 解：根据题意，将点A（-1，2），B（2，-3）代入直线y=kx+b，
得：$\left\{\begin{array}{l}{-k+b=2}\\{2k+b=-3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\frac{5}{3}}\\{b=\frac{1}{3}}\end{array}\right.$，
∴由反比例函数的性质可知，k=-$\frac{5}{3}$＜0时，函数y=$\frac{k}{x}$的图象在第二、四象限，
故选：C．
点评 本题主要考查待定系数法求一次函数解析式及反比例函数的图象与性质，熟练掌握待定系数法与反比例函数的图象与性质是解题的关键．
练习册系列答案
相关题目
向某一容器中注水，注满为止，表示注水量与水深的函数关系的图象大致如图所示，则该容器可能是（ ）
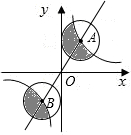如图，正比例函数y=2x的图象和反比例函数$y=\frac{8}{x}$的图象相交于A、B两点，以A、B为圆心的两圆均与y轴相切，则图中阴影部分的面积之和等于（ ）
画出如图所示几何体的主视图和左视图．
如图是由我市某中学楼层间的两个台阶组成的几何体，已知两个台阶的高度和宽度是相同的，据此可判断此几何体的三视图是（ ）
3．函数y=$\frac{x+3}{\sqrt{x-2}}$中，自变量x的取值范围是（ ）
| A． | x＞2 | B． | x≥-3 | C． | x＞-3 | D． | x≥2 |
10．
如图，已知一条直线经过点A（0，2），点B（1，0），将这条直线向左平移与x轴、y轴分别交于点C、点D，若DB=DC，则直线CD的函数解析式为（ ）
如图，已知一条直线经过点A（0，2），点B（1，0），将这条直线向左平移与x轴、y轴分别交于点C、点D，若DB=DC，则直线CD的函数解析式为（ ）| A． | y=-x+2 | B． | y=-2x-2 | C． | y=2x+2 | D． | y=-2x+2 |
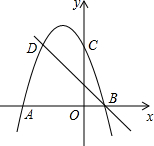如图，二次函数的图象与x轴交于点A（-3，0），B（1，0），交y轴于点C（0，3），点C，D是二次函数图象上关于抛物线对称轴的一对对称点，一次函数的图象过点B，D．