题目内容
8.(1)计算:$\sqrt{75}$×$\sqrt{\frac{1}{3}}$+(-$\frac{1}{2}$)-1-|$\sqrt{2}$-2|-$\sqrt{3}$tan60°;(2)先化简,再求值:$\frac{1}{x}$÷($\frac{{x}^{2}+1}{x+1}$-x+1),然后从-1≤x<2中选取一个合适的数作为x的值代入求值.
分析 (1)先化简各二次根式、负指数幂、去绝对值符号、代入三角函数值,再依据混合运算顺序计算可得;
(2)先计算括号内分式的减法,再计算除法.
解答 解:(1)原式=5$\sqrt{3}$×$\frac{\sqrt{3}}{3}$-2-(2-$\sqrt{2}$)-$\sqrt{3}$×$\sqrt{3}$
=5-2-2+$\sqrt{2}$-3
=$\sqrt{2}$-2;
(2)原式=$\frac{1}{x}$÷($\frac{{x}^{2}+1}{x+1}$-$\frac{{x}^{2}-1}{x+1}$)
=$\frac{1}{x}$÷$\frac{2}{x+1}$
=$\frac{1}{x}$•$\frac{x+1}{2}$
=$\frac{x+1}{2x}$,
当x=1时,原式=$\frac{2}{2}$=1.
点评 本题主要考查二次根式的混合运算及分式的化简求值,熟练掌握运算法则和运算顺序是关键.

练习册系列答案
相关题目
18.若点A(-1,2),B(2,-3)在直线y=kx+b上,则函数y=$\frac{k}{x}$的图象在( )
| A. | 第一、三象限 | B. | 第一、二象限 | C. | 第二、四象限 | D. | 第二、三象限 |
18.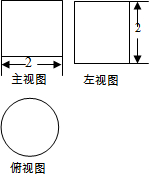 如图是某几何体的三视图,下列判断正确的是( )
如图是某几何体的三视图,下列判断正确的是( )
 如图是某几何体的三视图,下列判断正确的是( )
如图是某几何体的三视图,下列判断正确的是( )| A. | 几何体是圆柱体,高为2 | B. | 几何体是圆锥体,高为2 | ||
| C. | 几何体是圆柱体,半径为2 | D. | 几何体是圆锥体,直径为2 |
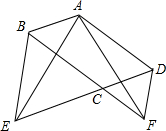 如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF.
如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF. 如图,已知A(-4,n),B(-1,2)是一次函数y=kx+b与反比例函数$y=\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,n),B(-1,2)是一次函数y=kx+b与反比例函数$y=\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D. 如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )



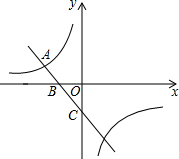 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a). 如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°.
如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°.