题目内容
18.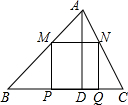 锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )
锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )| A. | 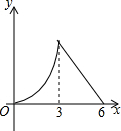 | B. | 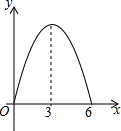 | C. |  | D. | 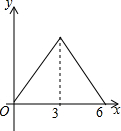 |
分析 根据题意可以表示出矩形的面积y与自变量x之间的函数关系式,从而可以得到y关于x的函数图象,本题得以解决.
解答 解:作AD⊥BC于点D,交MN于点E,如下图所示,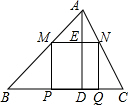
∵锐角△ABC中,BC=6,S△ABC=12,
∴$\frac{AD×BC}{2}=\frac{AD×6}{2}=12$,
解得,AD=4,
∵两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,
∴MP=ED,△AMN∽△ABC,
∴$\frac{AE}{AD}=\frac{MN}{BC}$
又∵MN的长为x,矩形MPQN的面积为y,
∴$\frac{AE}{4}=\frac{x}{6}$
解得,AE=$\frac{2x}{3}$,
∴ED=AD-AE=4-$\frac{2x}{3}$,
∴MP=$4-\frac{2x}{3}$,
∴矩形的面积y=x($4-\frac{2x}{3}$)=$-\frac{2}{3}{x}^{2}+4x$=$-\frac{2}{3}(x-3)^{2}+6$,
∴y关于x的函数图象是二次函数,顶点坐标是(3,6),
故选B.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,可以列出相应的函数关系式,得到相应的函数的图象.

练习册系列答案
相关题目
8.下列商标是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.下列方程中,有两个相等的实数根的是( )
| A. | x2-4x+4=0 | B. | x2-2x+5=0 | C. | x2-2x=0 | D. | x2-2x-1=0 |
10.下列判断正确的是( )
| A. | “打开电视机,正在播百家讲坛”是必然事件 | |
| B. | “在标准大气压下,水加热到100℃会沸腾”是必然事件 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | “篮球运动员在罚球线上投篮一次,未投中”是不可能事件 |
8. 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据以上图表信息解答下列问题:
(1)频数分布表中的m=48,n=0.3;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108°;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是$\frac{1}{6}$.
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 60 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 72 | n |
| 跳绳 | 36 | 0.15 |
| 其它 | 24 | 0.10 |
(1)频数分布表中的m=48,n=0.3;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108°;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是$\frac{1}{6}$.
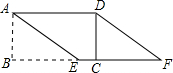 如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.