题目内容
15.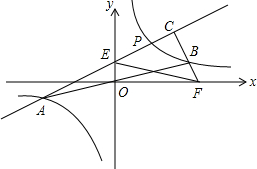 已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.
已知双曲线y=$\frac{k}{x}$(k>0)与直线y=$\frac{1}{k}$x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m=1.
分析 先求出A、B两点坐标,设点P(a,$\frac{k}{a}$),求出直线AP、BC得E、F两点坐标,利用两点间距离公式列出方程即可解决.
解答 解:由$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=\frac{1}{k}x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=k}\\{y=1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-k}\\{y=-1}\end{array}\right.$,
∴点A(-k,-1),B(k,1),
设点P(a,$\frac{k}{a}$),则直线AP为y=$\frac{1}{a}x+\frac{k}{a}-1$,直线BC为y=-ax+ak+1,
∴点E坐标(0,$\frac{k}{a}$-1),F坐标(k+$\frac{1}{a}$,0),
∵AE2+BF2=m•EF2,
∴k2+($\frac{k}{a}$)2+$\frac{1}{{a}^{2}}$+1=m[(k+$\frac{1}{a}$)2+($\frac{k}{a}$-1)2]
∴m(k2+($\frac{k}{a}$)2+$\frac{1}{{a}^{2}}$+1)=k2+($\frac{k}{a}$)2+$\frac{1}{{a}^{2}}$+1,
∴m=1.
故答案为1.
(补充方法:作AM∥BF交x轴于M,连接EM,只要证明△BOF≌△AOM,可得OF=OM,推出EM=EF,即可解决问题)
点评 本题考查一次函数、反比例函数以及勾股定理等有关知识,学会利用方程组求交点坐标,解题的关键是设参数a,想办法表示点E、F的坐标,题目有难度,有两个参数a、k,属于中考填空题中的压轴题.

 智能训练练测考系列答案
智能训练练测考系列答案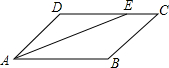 如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )
如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0.5 |
| A. | “打开电视机,正在播百家讲坛”是必然事件 | |
| B. | “在标准大气压下,水加热到100℃会沸腾”是必然事件 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | “篮球运动员在罚球线上投篮一次,未投中”是不可能事件 |
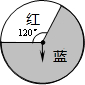 一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )
一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )| A. | 转出的结果一定是“蓝色” | |
| B. | 转出的结果为“蓝色”的可能性大于“红色” | |
| C. | 转出的结果为“红色”的可能性大于“蓝色” | |
| D. | 转出的结果为“蓝色”和“红色”的可能性一样大 |
| A. | 摸出的三个球中至少有一个球是白球 | |
| B. | 摸出的三个球中至少有一个球是黑球 | |
| C. | 摸出是三个球中至少有两个球的黑球 | |
| D. | 摸出的单个球中至少有两个球是白球 |
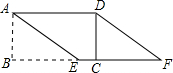 如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD. 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.