题目内容
5.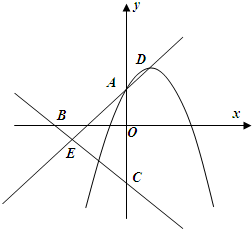 如图,抛物线y=-x2+2x+m(m>0)与y轴交于A,顶点为D,直线y=-$\frac{1}{2}$x-2m分别与x轴、y轴交于B、C两点,与直线AD相交于E点.
如图,抛物线y=-x2+2x+m(m>0)与y轴交于A,顶点为D,直线y=-$\frac{1}{2}$x-2m分别与x轴、y轴交于B、C两点,与直线AD相交于E点.(1)求A、D的坐标(用m的代数式表示);
(2)将△EAC沿着y轴翻折,若点E的对称点P恰好落在抛物线上,求m的值;
(3)若在抛物线y=-x2+2x+m(m>0)上存在点P,使得以P、A、C、E为顶点的四边形是平行四边形,求此抛物线的解析式.
分析 (1)利用配方法求出顶点D坐标,令x=0,可以求出点A坐标.
(2)求出直线AC解析式,利用方程组求出点E坐标,再求出点E关于y轴对称点E′坐标,利用待定系数法即可解决问题.
(3)分AC为边,AC为对角线两种情形分别讨论即可解决问题.
解答 解:(1)∵y=-x2+2x+m=-(x-1)2+m+1,
∴顶点D(1,m+1),
令x=0,则y=m,
∴点A(0,m),
∴A(0,m),D(1,m+1).
(2)设直线AD为y=kx+b,则$\left\{\begin{array}{l}{b=m}\\{k+b=m+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=m}\end{array}\right.$,
∴直线AD解析式为y=X+m,
由$\left\{\begin{array}{l}{y=x+m}\\{y=-\frac{1}{2}x-2m}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2m}\\{y=-m}\end{array}\right.$,
∴点E坐标为(-2m,-m),
∴点E关于y轴的对称点E′(2m,-m),
∵点E′在抛物线上,
∴-m=-4m2+4m+m,
∴m=$\frac{3}{2}$或0,
∵m>0,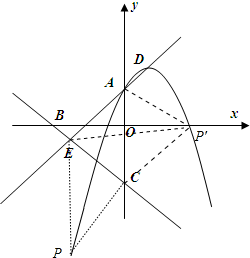
∴m=$\frac{3}{2}$
(3)如图,
①当AC为边时,EP∥AC,EP=AC,
∴点P坐标(-2m,-4m),
∴-4m=-4m2-4m+m,
∴m=$\frac{1}{4}$或0(舍弃),
②当AC为对角线时,点P′坐标(2m,0),
∴0=-4m2+4m+m,
∴m=$\frac{5}{4}$或0(舍弃)
∴抛物线解析式为y=-x2+2x+$\frac{5}{4}$或y=-x2+2x+$\frac{1}{4}$.
点评 本题考查二次函数综合题、一次函数、对称、平行四边形的判定和性质等知识,解题的关键是熟练掌握待定系数法,学会用配方法确定抛物线顶点坐标,学会分类讨论,知道可以利用方程组求两个函数图象交点坐标,属于中考压轴题.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案| 甲 | 乙 | 丙 | 丁 | |
| ∠C(单位:度) | 34 | 36 | 38 | 40 |
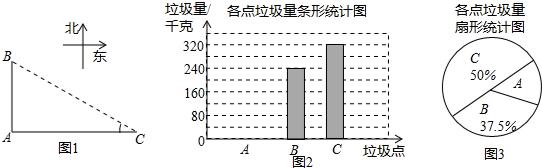
(1)求表中∠C度数的平均数$\overline{x}$;
(2)求A处的垃圾量,并将不完整的统计图2、3补充完整;
(3)用(1)中的$\overline{x}$作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
| A. | 直角三角形 | B. | 钝角 | C. | 线段 | D. | 圆 |
 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式.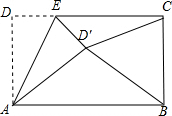 如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中:
如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中: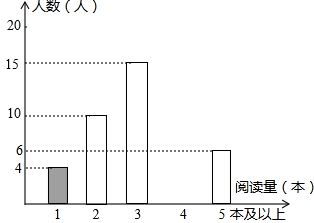 某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.