题目内容
2. 如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$.
如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$.
分析 要求平行四边形的周长就要先求出AB、AD的长,利用平行四边形的性质和勾股定理即可求出.
解答 解:∵∠EAF=45°,
∴∠C=360°-∠AEC-∠AFC-∠EAF=135°,
∴∠B=∠D=180°-∠C=45°,
则AE=BE,AF=DF,
设AE=x,则AF=2-x,
在Rt△ABE中,根据勾股定理可得,AB=$\sqrt{2}$x,
同理可得AD=$\sqrt{2}$(2-x).
则平行四边形ABCD的周长是2(AB+AD)=2[$\sqrt{2}$x+$\sqrt{2}$(2-x)]=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查了平行四边形的性质,解题关键是利用平行四边形的性质结合等角对等边、勾股定理来解决有关的计算和证明.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.小张笔记上有一道练习题(8a2+3ab-2b2)-(-2a2+ab-3b2)=10a2______+b2但空格处被墨水污染了,请问被污染的一项是( )
| A. | -2ab | B. | +2ab | C. | +4ab | D. | -4ab |
 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
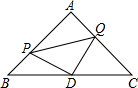 如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.