题目内容
19.设a,b,c为整数(a≠b),且|a-b|+|c-a|=1.(1)求|b-a|+|a-c|+|c-b|的值;
(2)若数轴上点A,B对应的数分别为a,b,从某时刻起点A,B同时出发,分别沿数轴的正,负方向匀速运动,点A的速度为2个单位长度/秒,点B的速度为3个单位长度/秒,经过多长时间A,B相距51个单位长度?
(2)若数轴上点A,B,D对应的数分别为a,b,d,当a=-3,且BD=$\frac{2}{3}$AD时,求点D所对应的数.
分析 (1)首先根据条件确定|a-b|≥1,|b-c|≥1,|a-c|≥0,再由|a-b|+|c-a|=1可得c=a,|a-b|=1,进而可得答案;
(2)此题要分两种情况:①a在b的左侧,相隔1个单位;②a在b的右侧,相隔1个单位,再根据速度×时间=路程可列出方程;
(3)此题要分4种情况:①当a=-3,b=-2时,D在AB之间;D在B的右侧;②当a=-3,b=-4时,D在AB之间;D在B的左侧.
解答 解:(1)∵a、b、c为整数,a≠b,
∴|a-b|≥1,|b-c|≥1,|a-c|≥0,
∵|a-b|+|c-a|=1
∴c-a=0,|a-b|=1,
∴a=c,
∴|b-a|+|a-c|+|c-b|=1+0+1=2;
(2)如图1: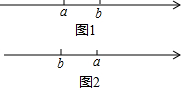 由题意得:(2+3)t-1=52,
由题意得:(2+3)t-1=52,
解得:t=$\frac{52}{5}$;
如图2:由题意得:5t+1=51,
解得:t=10;
答:经过$\frac{52}{5}$秒或10秒时间A,B相距51个单位长度;
(3) 若数轴上点A,B,D对应的数分别为a,b,d,当a=-3,且BD=$\frac{2}{3}$AD时,求点D所对应的数
若数轴上点A,B,D对应的数分别为a,b,d,当a=-3,且BD=$\frac{2}{3}$AD时,求点D所对应的数
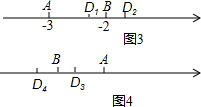
如图3,当a=-3,b=-2时,
∵BD=$\frac{2}{3}$AD,
∴D1=-2.4;D2=0;
如图4,当a=-3,b=-4时,
∵BD=$\frac{2}{3}$AD,
∴D1=-3.6;D2=-6.
点评 此题主要考查了一元一次方程的应用和数轴,关键是正确理解题意,找出题目中的等量关系,注意要分情况进行讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.小张笔记上有一道练习题(8a2+3ab-2b2)-(-2a2+ab-3b2)=10a2______+b2但空格处被墨水污染了,请问被污染的一项是( )
| A. | -2ab | B. | +2ab | C. | +4ab | D. | -4ab |
8.若二次函数y=ax2+$\sqrt{2}$(a≠0),当x分别取x1,x2时,函数值相等,则当x取x1+x2时,函数值为( )
| A. | 0 | B. | a | C. | $\sqrt{2}$ | D. | 不确定 |
9.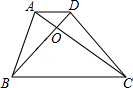 如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
 如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 11:20 |
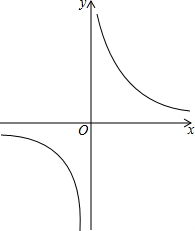 反比例函数y=$\frac{k-1}{x}$如图,则:
反比例函数y=$\frac{k-1}{x}$如图,则: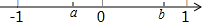 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
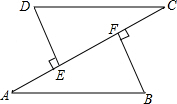 已知:如图,AE=CF,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.求证:AB∥CD.
已知:如图,AE=CF,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.求证:AB∥CD.