题目内容
14.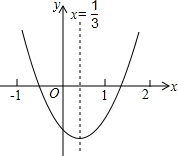 从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据二次函数的图象以及性质即可求出答案.
解答 解:①由抛物线与y轴的交点可知:c<0,故①正确;
②由抛物线的开口方向可知:a>0,
-$\frac{b}{2a}$>0,
∴b<0,
∴abc>0,故②正确;
③令x=1代入y=ax2+bx+c,
∴y=a-b+c<0,故③错误;
④由对称轴可知:-$\frac{b}{2a}$<1,
∵a>0,
∴-b<2a
∴2a+b>0,故④正确
⑤令x=2代入y=ax2+bx+c,
∴y=4a+2b+c>0,故⑤正确;
故选(C)
点评 本题考查二次函数的性质,解题的关键是熟练运用二次函数图象及性质,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在下列几个几何体中,主视图与俯视图都是圆的是( )
| A. | 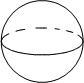 | B. | 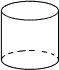 | C. |  | D. | 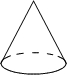 |
19.下列说法中,正确的是( )
| A. | 任何数都有两个平方根 | B. | 9的平方根只有3 | ||
| C. | (-2)3的立方根为2 | D. | 0.04的算术平方根为0.2 |
4.下列方程,不适宜用因式分解法求解的是( )
| A. | x2=3x | B. | (x-2)2=3x-6 | C. | 4x2+4x+1=0 | D. | (x+2)(2x-1)=5 |
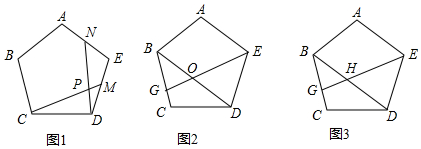
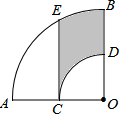 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.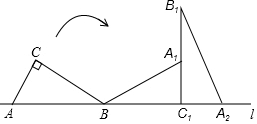 如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π.
如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π. 如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.
如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.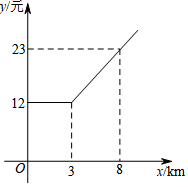 为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:
为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题: