题目内容
1. 如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4000米到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4000米到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )| A. | 2000米 | B. | 3000米 | C. | 4000米 | D. | 5000米 |
分析 根据题意可得∠ABC=90°,AB=4000米,BC=3000米,然后利用勾股定理求得AC.
解答  解:如图,连接AC.
解:如图,连接AC.
依题意得:∠ABC=90°,AB=4000米,BC=3000米,
则由勾股定理,得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{400{0}^{2}+300{0}^{2}}$=5000(米)
故选:D.
点评 本题考查勾股定理在实际生活中的运用,关键是得出两船行驶的路程和两船的距离构成的是直角三角形,然后根据勾股定理可求出解.

练习册系列答案
相关题目
12.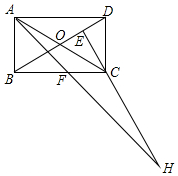 在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF与EC交于点H,下列结论中:①AF=FH;②BO=BF;③AC=HC;④BE=3DE,正确的是( )
在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF与EC交于点H,下列结论中:①AF=FH;②BO=BF;③AC=HC;④BE=3DE,正确的是( )
 在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF与EC交于点H,下列结论中:①AF=FH;②BO=BF;③AC=HC;④BE=3DE,正确的是( )
在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF与EC交于点H,下列结论中:①AF=FH;②BO=BF;③AC=HC;④BE=3DE,正确的是( )| A. | ②④ | B. | ③④ | C. | ②③④ | D. | ①②③④ |
16.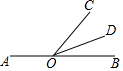 如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为( )
如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为( )
 如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为( )
如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为( )| A. | 30° | B. | 31° | C. | 30°30′ | D. | 31°30′ |
10.下列计算正确的是( )
| A. | 3a2+2a2=5a4 | B. | a•a=a2 | C. | 4a6÷2a2=2a3 | D. | 2a-a=2 |
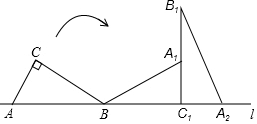 如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π.
如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π. 如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.
如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.