题目内容
19.已知圆锥的母线长为30cm,其侧面展开图的圆心角为120°,则该圆锥的底面半径为10cm.分析 由于圆锥的母线长为30cm,侧面展开图是圆心角为120°扇形,设圆锥底面半径为rcm,那么圆锥底面圆周长为2πrcm,所以侧面展开图的弧长为2πrcm,然后利用扇形的面积公式即可得到关于r的方程,解方程即可求解
解答 解:设圆锥底面半径为rcm,
那么圆锥底面圆周长为2πrcm,
所以侧面展开图的弧长为2πrcm,
S圆锥侧面积=$\frac{1}{2}$×2πr×30=$\frac{120π×3{0}^{2}}{360}$,
解得:r=10,
故答案为:10.
点评 本题主要考查圆锥侧面展开图的知识和圆锥侧面面积的计算;正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
14.在△ABC中,BC=a,AB=c,CA=b.且a、b、c满足:a2-8b=-23,b2-10c=-34,c2-6a=7,则2sinA+sinB=( )
| A. | 1 | B. | $\frac{7}{5}$ | C. | 2 | D. | $\frac{12}{5}$ |
11.若一次函数y=kx+b的图象交y轴于正半轴,且y的值随x值的增大而减小,则( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |


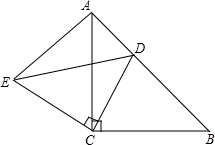 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,