题目内容
如图,点B是x轴正半轴上一动点,点A是线段OB垂直平分线上的点,P为y轴正半轴上一动点,且∠OPB=∠OAB=α(α为锐角).

(1)求证:∠AOP=∠ABP;
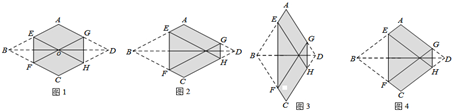
(2)如图1,若∠AOB=60°,PO=2,求:①PB的长;②PA的长.
(3)已知,点A的纵坐标是3,问当点B在x轴正半轴上移动时(如图2),PO+PB的长是否会发生改变?若不变,求出PO+PB的值;若会改变,请说明理由.

(1)求证:∠AOP=∠ABP;
(2)如图1,若∠AOB=60°,PO=2,求:①PB的长;②PA的长.
(3)已知,点A的纵坐标是3,问当点B在x轴正半轴上移动时(如图2),PO+PB的长是否会发生改变?若不变,求出PO+PB的值;若会改变,请说明理由.
考点:全等三角形的判定与性质,坐标与图形性质,线段垂直平分线的性质,等边三角形的判定与性质
专题:计算题
分析:(1)由已知角相等,以及对顶角相等,利用三角形内角和定理即可得证;
(2)由点A是线段OB垂直平分线上的点,得到OA=AB,再由∠AOB=60°,得到三角形AOB为等边三角形,利用等边三角形三内角为60°得到∠OPB=∠OAB=∠OBA=60°,根据∠POB=90°,得到∠OBP=30°,利用30度所对的直角边等于斜边的一半得到PB=2OP,求出PB的长,且BM为平分线,利用三线合一得到BM垂直于OA,且AM=OM,即可得到PA=OP=2;
(3)PO+PB的长不变,理由为:延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴,由OA=AB,利用等边对等角得到∠AOB=∠ABO,再由∠ABO+∠ODB=∠AOB+∠AOD=90°,得到∠AOD=∠ODB,进而确定出∠ODB=∠ABP,利用等角对等边得到AD=OA,BP=PD,即E为OD中点,即可确定出PO+PB的长.
(2)由点A是线段OB垂直平分线上的点,得到OA=AB,再由∠AOB=60°,得到三角形AOB为等边三角形,利用等边三角形三内角为60°得到∠OPB=∠OAB=∠OBA=60°,根据∠POB=90°,得到∠OBP=30°,利用30度所对的直角边等于斜边的一半得到PB=2OP,求出PB的长,且BM为平分线,利用三线合一得到BM垂直于OA,且AM=OM,即可得到PA=OP=2;
(3)PO+PB的长不变,理由为:延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴,由OA=AB,利用等边对等角得到∠AOB=∠ABO,再由∠ABO+∠ODB=∠AOB+∠AOD=90°,得到∠AOD=∠ODB,进而确定出∠ODB=∠ABP,利用等角对等边得到AD=OA,BP=PD,即E为OD中点,即可确定出PO+PB的长.
解答: (1)证明:∵∠OPB=∠OAB,且∠OMP=∠AMB,
(1)证明:∵∠OPB=∠OAB,且∠OMP=∠AMB,
∴∠AOP=∠ABP;
(2)解:∵点A为OB垂直平分线上的点,
∴OA=AB,
∵∠AOB=60°,
∴△AOB为等边三角形,
∴∠OPB=∠OAB=∠OBA=60°,
∵∠POB=90°,
∴∠OBP=30°,
∴PB=2OP=4,BM平分∠ABO,
∴BM⊥OA,AM=OM,
∴PA=OP=2;
(3)解:PO+PB的长不变,理由为:
延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴;
∵OA=AB,
∴∠AOB=∠ABO,
∵∠ABO+∠ODB=∠AOB+∠AOD=90°,
∴∠AOD=∠ODB,
∴∠ODB=∠ABP,
∴AD=OA,BP=PD,
∴E为OD中点,
∵OE=AH=3,
∴PO+PB=PO+PD=OP+PE+DE=2AH=6.
 (1)证明:∵∠OPB=∠OAB,且∠OMP=∠AMB,
(1)证明:∵∠OPB=∠OAB,且∠OMP=∠AMB,∴∠AOP=∠ABP;
(2)解:∵点A为OB垂直平分线上的点,
∴OA=AB,
∵∠AOB=60°,
∴△AOB为等边三角形,
∴∠OPB=∠OAB=∠OBA=60°,
∵∠POB=90°,
∴∠OBP=30°,
∴PB=2OP=4,BM平分∠ABO,
∴BM⊥OA,AM=OM,
∴PA=OP=2;
(3)解:PO+PB的长不变,理由为:
延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴;
∵OA=AB,
∴∠AOB=∠ABO,
∵∠ABO+∠ODB=∠AOB+∠AOD=90°,
∴∠AOD=∠ODB,
∴∠ODB=∠ABP,
∴AD=OA,BP=PD,
∴E为OD中点,
∵OE=AH=3,
∴PO+PB=PO+PD=OP+PE+DE=2AH=6.
点评:此题考查了全等三角形的判定与性质,等边三角形的判定与性质,以及线段垂直平分线定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列运算,正确的是( )
| A、2a+3b=5ab |
| B、a3•a2=a5 |
| C、a6÷a2=a3 |
| D、a3+a2=a5 |
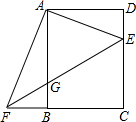 如图,在矩形ABCD中,AB=8,BC=6,点E是边CD上一个动点(点E与点C、点D不重合),连接AE,作AF⊥AE,交直线CB于点F,连接EF,交边AB于点G.设DE=x,BF=y.
如图,在矩形ABCD中,AB=8,BC=6,点E是边CD上一个动点(点E与点C、点D不重合),连接AE,作AF⊥AE,交直线CB于点F,连接EF,交边AB于点G.设DE=x,BF=y. 如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识
如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识 如图,某景点在山顶C处,以前人们从A处出发沿着坡比为1:2的缓坡AB爬行200米到达B处,再由B处沿着坡角为60°的陡坡BC蹬阶180米到达C处,整个路程比较危险.后来管理部门在A、C之间架设了索道,已知索道AC与水平面AE的夹角为45°,求索道AC的长.
如图,某景点在山顶C处,以前人们从A处出发沿着坡比为1:2的缓坡AB爬行200米到达B处,再由B处沿着坡角为60°的陡坡BC蹬阶180米到达C处,整个路程比较危险.后来管理部门在A、C之间架设了索道,已知索道AC与水平面AE的夹角为45°,求索道AC的长.