Question

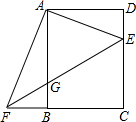如图，在矩形ABCD中，AB=8，BC=6，点E是边CD上一个动点（点E与点C、点D不重合），连接AE，作AF⊥AE，交直线CB于点F，连接EF，交边AB于点G．设DE=x，BF=y．
（1）求y关于x的函数关系式，并且直接写出x的取值范围；
（2）如果△AEF∽△DEA，试证明：BF=AD；
（3）当E点在CD上运动时，△AEG能否成为以EG为一腰的等腰三角形？如果能，试求出DE的长；如果不能，请说明理由．

Answer 1

考点：相似形综合题

专题：

分析：（1）由矩形的性质推出∠BAD=∠D=∠ABC=90°，即得∠D=∠ABF，再由AF⊥AE得出∠EAF=∠BAD=90°，然后由∠EAF=∠BAF+∠BAE，∠BAD=∠DAE+∠BAE，得出∠DAE=∠BAF，由∠D=∠ABF，∠DAE=∠BAF，得△DAE∽△BAF，再由三角形相似的性质得到y关于x的函数解析式，从而求出x的取值范围．
（2）由△AEF∽△DEA，△DAE∽△BAF．可以得到对应的角相等，推导出线段相等，利用线段成比例确定点G为线段EF的中点，借用比例线段即可得到答案．
（3）当点E在边CD上移动时，△AEG能成为以EG为一腰的等腰三角形，此时可以推断出两种情况，一一推断即可．

解答：解：（1）在矩形ABCD中，∠BAD=∠D=∠ABC=90°，AD=BC=6．
即得∠D=∠ABF．
∵AF⊥AE，
∴∠EAF=∠BAD=90°．
又∵∠EAF=∠BAF+∠BAE，∠BAD=∠DAE+∠BAE，
∴∠DAE=∠BAF．
于是，由∠D=∠ABF，∠DAE=∠BAF，
得△DAE∽△BAF．
∴

AD

AB

=

DE

EF

∵DE=x，BF=y，
∴

3

4

=

x

y

，
∴y关于x的函数解析式是y=

4

3

x，0＜x＜4．

（2）∵△AEF∽△DEA，
∴∠EAF=∠D，∠AFE=∠DAE，∠FAE=∠DEA，
由（1）知道△DAE∽△BAF
∴∠FAG=∠AFG，∠GAE=∠GEA，
∴GF=GA=GE，
在矩形ABCD中，AB∥CD，

FG

GE

=

FB

BC

=1．
即得FB=BC．
又∵AD=BC，
∴FB=AD；

（3）当E点在CD上运动时，△AEG能成为以EG为一腰的等腰三角形．
（a）当GE=GA时，∠GAE=∠GEA，
∠GAE+∠FAG=90°，
∠GEA+∠AFG=90°，
∴∠AFG=∠FAG，所以GA=GF，
所以G是FE的中点，
由（2）知道FB=BC=6，
y关于x的函数解析式是y=

4

3

x，
∴DE=

9

2

．
（b）当EA=EG时，△AFB∽△FGB，
GB=

2

9

x²，
∵GB∥EC，
∴CE=5，
∴DE=3．

点评：本题主要考查了矩形的性质以及相似三角形的判定和性质的综合应用，一次函数解析式的求法也是解题的关键．