题目内容
阅读下面材料:
在学习小组活动中,小明探究了下面问题:菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点处,折痕分别为EF、GH.当重合点在对角线BD上移动时,六边形AEFCHG的周长的变化情况是怎样的?
小明发现:若∠ABC=60°,
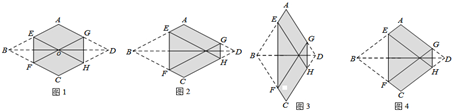
①如图1,当重合点在菱形的对称中心O处时,六边形AEFCHG的周长为 ;
②如图2,当重合点在对角线BD上移动时,六边形AEFCHG的周长 (填“改变”或“不变”).
请帮助小明解决下面问题:
如果菱形纸片ABCD边长仍为2,改变∠ABC的大小,折痕EF的长为m.
(1)如图3,若∠ABC=120°,则六边形AEFCHG的周长为 ;
(2)如图4,若∠ABC的大小为2α,则六边形AEFCHG的周长可表示为 .
在学习小组活动中,小明探究了下面问题:菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点处,折痕分别为EF、GH.当重合点在对角线BD上移动时,六边形AEFCHG的周长的变化情况是怎样的?
小明发现:若∠ABC=60°,

①如图1,当重合点在菱形的对称中心O处时,六边形AEFCHG的周长为
②如图2,当重合点在对角线BD上移动时,六边形AEFCHG的周长
请帮助小明解决下面问题:
如果菱形纸片ABCD边长仍为2,改变∠ABC的大小,折痕EF的长为m.
(1)如图3,若∠ABC=120°,则六边形AEFCHG的周长为
(2)如图4,若∠ABC的大小为2α,则六边形AEFCHG的周长可表示为
考点:翻折变换(折叠问题),菱形的性质
专题:
分析:①根据题意可知△BEF和△DGH是等边三角形,再根据菱形的性质即可求解;
②根据题意可知△BEF和△DGH是等边三角形,再根据菱形的性质即可求解;
(1)根据题意可知EF+GH=AC,再根据三角函数和菱的性质即可求解;
(2)根据题意可知EF+GH=AC,再根据三角函数和菱形的性质即可求解.
②根据题意可知△BEF和△DGH是等边三角形,再根据菱形的性质即可求解;
(1)根据题意可知EF+GH=AC,再根据三角函数和菱的性质即可求解;
(2)根据题意可知EF+GH=AC,再根据三角函数和菱形的性质即可求解.
解答:解:①如图1,当重合点在菱形的对称中心O处时,
由题意可知△BEF和△DGH是等边三角形,
∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=2+2+2=6.
∴六边形AEFCHG的周长为 6;
②如图2,当重合点在对角线BD上移动时,
由题意可知△BEF和△DGH是等边三角形,
∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=2+2+2=6.
∴六边形AEFCHG的周长为6.
故六边形AEFCHG的周长不变.
(1)如图3,若∠ABC=120°,
由题意可知EF+GH=AC,
则六边形AEFCHG的周长为2×2+2×sin60°×2=4+2
;
(2)如图4,若∠ABC的大小为2α,
由题意可知EF+GH=AC,
则六边形AEFCHG的周长可表示为2×2+2×sinα×2=4+4sinα.
故答案为:①6;②不变.(1)4+2
;(2)4+4sinα.
由题意可知△BEF和△DGH是等边三角形,
∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=2+2+2=6.
∴六边形AEFCHG的周长为 6;
②如图2,当重合点在对角线BD上移动时,
由题意可知△BEF和△DGH是等边三角形,
∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=2+2+2=6.
∴六边形AEFCHG的周长为6.
故六边形AEFCHG的周长不变.
(1)如图3,若∠ABC=120°,
由题意可知EF+GH=AC,
则六边形AEFCHG的周长为2×2+2×sin60°×2=4+2
| 3 |
(2)如图4,若∠ABC的大小为2α,
由题意可知EF+GH=AC,
则六边形AEFCHG的周长可表示为2×2+2×sinα×2=4+4sinα.
故答案为:①6;②不变.(1)4+2
| 3 |
点评:考查了翻折变换(折叠问题),菱形的性质,本题关键是得到EF+GH=AC,综合性较强,有一定的难度.

练习册系列答案
相关题目
对于数据组3,3,2,3,6,3,10,3,6,3,2.这组数据的平均数与众数分别为( )
| A、4,3 | B、3,3 |
| C、4.5,2 | D、5,6 |
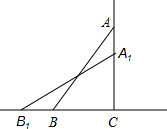 如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)
如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数) 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.