题目内容
在3点钟和4点钟之间,时钟上的分针和时针在何时反向成一直线?
考点:一元一次方程的应用
专题:
分析:从圆心角的角度看,钟面圆周一周是360°,分针一小时(60分)转一周,那么每分钟转:360°÷60=6°;时针一小时(60分)转:360°÷12=30°,那么每分钟转:30°÷60=0.5°;在3点整时,分针落后时针的角度是:30°×3=90°,假设时针不动,分针只要再追赶180°+90°=270°(路程差),这时时针与分针就成直线;再根据速度差为:6°-0.5°=5.5°,设3点x分时时钟上的分针和时针在何时反向成一直线,根据题意列出方程(6°-0.5°)x=180°+90°,解方程即可.
解答:解:分针每分钟转:360°÷60=6°;时针一小时(60分)转:360°÷12=30°,那么每分钟转:30°÷60=0.5°;
由题意,得(6°-0.5°)x=180°+90°,
解得x=49
.
答:在3点49
分时,时钟上的分针和时针在何时反向成一直线.
由题意,得(6°-0.5°)x=180°+90°,
解得x=49
| 1 |
| 11 |
答:在3点49
| 1 |
| 11 |
点评:本题考查了时间与钟面问题中钟面追及问题,关键是求出追及的路程(用角度表示)和速度差(用角度表示).

练习册系列答案
相关题目
如果关于x的一元二次方程x2-6x=2k有两个实数根,那么实数k的取值范围是( )
A、k≤-
| ||
B、k<-
| ||
C、k≥-
| ||
D、k>-
|
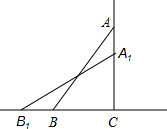 如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)
如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)
 如图,在Rt△ABC中,∠C=90°,点D是AC边上一点,tan∠DBC=
如图,在Rt△ABC中,∠C=90°,点D是AC边上一点,tan∠DBC= 如图,从电线杆离地面3米处向地面拉一条长为5米的拉线,这条拉线在地面的固定点距离电线杆底部有
如图,从电线杆离地面3米处向地面拉一条长为5米的拉线,这条拉线在地面的固定点距离电线杆底部有