题目内容
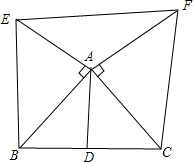 已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.
已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:延长AD至点G,使得AD=DG,连接BG,CG,易证四边形ABGC是平行四边形,即可求得∠EAF=∠ABG,即可求证△EAF≌△BAG,即可解题.
解答:证明:延长AD至点G,使得AD=DG,连接BG,CG,
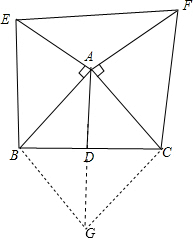
∵AD=DG,BD=CD,
∴四边形ABGC是平行四边形,
∴AC=AF=BG,AB=AE=CG,∠BAC+∠ABG=180°,
∵∠EAF+∠BAC=180°,
∴∠EAF=∠ABG,
在△EAF和△BAG中,
,
∴△EAF≌△BAG(SAS),
∴EF=AG,
∵AG=2AD,
∴EF=2AD.

∵AD=DG,BD=CD,
∴四边形ABGC是平行四边形,
∴AC=AF=BG,AB=AE=CG,∠BAC+∠ABG=180°,
∵∠EAF+∠BAC=180°,
∴∠EAF=∠ABG,
在△EAF和△BAG中,
|
∴△EAF≌△BAG(SAS),
∴EF=AG,
∵AG=2AD,
∴EF=2AD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△EAF≌△BAG是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数y=(m+2)x2-2x-1的图象与x轴有交点,则k的取值范围是( )
| A、m>-3 |
| B、m≥-3 |
| C、m>-3且m≠-2 |
| D、m≥-3且m≠-2 |
 如图,AD∥EF∥BC,EF分别与AB,DC,AC,BD相交于点E、F、G、H,EH与FG相等吗?为什么?
如图,AD∥EF∥BC,EF分别与AB,DC,AC,BD相交于点E、F、G、H,EH与FG相等吗?为什么? 尺规画图 (不用写作法,要保留作图痕迹)
尺规画图 (不用写作法,要保留作图痕迹) 在Rt△ABC中,∠ACB=90°,AC=
在Rt△ABC中,∠ACB=90°,AC= 如图,已知直角梯形OABC的边OA在y轴的正半轴,OC在x轴的正半轴上,OA=AB=2,OC=3,D点是x轴正半轴的一动点,过点B作BE⊥BD交y轴的正半轴于点E.
如图,已知直角梯形OABC的边OA在y轴的正半轴,OC在x轴的正半轴上,OA=AB=2,OC=3,D点是x轴正半轴的一动点,过点B作BE⊥BD交y轴的正半轴于点E.