题目内容
 如图,已知直角梯形OABC的边OA在y轴的正半轴,OC在x轴的正半轴上,OA=AB=2,OC=3,D点是x轴正半轴的一动点,过点B作BE⊥BD交y轴的正半轴于点E.
如图,已知直角梯形OABC的边OA在y轴的正半轴,OC在x轴的正半轴上,OA=AB=2,OC=3,D点是x轴正半轴的一动点,过点B作BE⊥BD交y轴的正半轴于点E.(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CD的长;
(3)若D(1,0),过点D的直线交AB于点P,交(1)中的抛物线在第一象限的部分于点Q,且使三角形PCD为等腰三角形,求Q的坐标.
考点:二次函数综合题
专题:
分析:(1)根据OA、AB、OC的长,即可得到A、B、C三点的坐标,进而可用待定系数法求出抛物线的解析式;
(2)此题要通过构造全等三角形求解;过B作BM⊥x轴于M,那么∠EBF=∠ABM=90°,根据同角的余角相等可得∠EBA=∠DBM;易知BM=OA=AB=2,由此可证得Rt△EBA≌Rt△DBM,则AE=DM;CM的长易求得,关键是DM即AE的长;设抛物线的顶点为G,由于G点在线段AB的垂直平分线上,若过G作GH⊥AB,则GH是△ABE的中位线,G点的坐标易求得,即可得到GH的长,从而可求出AE的长,即可由CD=CM+DM=AE+CM求出CD的长;
(3)分三种情况:①DC=DP;②DP=CP;③CD=CP;进行讨论,先得到Q的横坐标,进一步得到Q的坐标.
(2)此题要通过构造全等三角形求解;过B作BM⊥x轴于M,那么∠EBF=∠ABM=90°,根据同角的余角相等可得∠EBA=∠DBM;易知BM=OA=AB=2,由此可证得Rt△EBA≌Rt△DBM,则AE=DM;CM的长易求得,关键是DM即AE的长;设抛物线的顶点为G,由于G点在线段AB的垂直平分线上,若过G作GH⊥AB,则GH是△ABE的中位线,G点的坐标易求得,即可得到GH的长,从而可求出AE的长,即可由CD=CM+DM=AE+CM求出CD的长;
(3)分三种情况:①DC=DP;②DP=CP;③CD=CP;进行讨论,先得到Q的横坐标,进一步得到Q的坐标.
解答:解:(1)由题意可得A(0,2),B(2,2),C(3,0),
设所求抛物线的解析式为y=ax2+bx+c(a≠0),则
,
解得
.
故抛物线的解析式为y=-
x2+
x+2;
 (2)设抛物线的顶点为G,
(2)设抛物线的顶点为G,
则G(1,
),过点G作GH⊥AB,垂足为H,
则AH=BH=1,GH=
-2=
;
∵EA⊥AB,GH⊥AB,
∴EA∥GH;
∴GH是△BEA的中位线,
∴EA=2GH=
;
过点B作BM⊥OC,垂足为M,则BM=OA=AB;
∵∠EBD=∠ABM=90°,
∴∠EBA=∠DBM=90°-∠ABD,
在Rt△EBA与Rt△DBM中,
∴Rt△EBA≌Rt△DBM(ASA),
∴DM=EA=
;
∵CM=OC-OM=3-2=1,
∴CD=DM+CM=
;
(3)∵D(1,0),
∴CD=3-1=2,
①DC=DP,Q的横坐标为1,当x=1时,y=-
x2+
x+2=
,Q的坐标为(1,
);
②DP=CP,Q的横坐标为2,当x=2时,y=-
x2+
x+2=2,Q的坐标为(2,2);
③CD=CP,Q的横坐标为3,当x=3时,y=-
x2+
x+2=2,Q的坐标为(3,0)(不合题意舍去).
综上所述,Q的坐标为(1,
);(2,2).
设所求抛物线的解析式为y=ax2+bx+c(a≠0),则
|
解得
|
故抛物线的解析式为y=-
| 2 |
| 3 |
| 4 |
| 3 |
 (2)设抛物线的顶点为G,
(2)设抛物线的顶点为G,则G(1,
| 8 |
| 3 |
则AH=BH=1,GH=
| 8 |
| 3 |
| 2 |
| 3 |
∵EA⊥AB,GH⊥AB,
∴EA∥GH;
∴GH是△BEA的中位线,
∴EA=2GH=
| 4 |
| 3 |
过点B作BM⊥OC,垂足为M,则BM=OA=AB;
∵∠EBD=∠ABM=90°,
∴∠EBA=∠DBM=90°-∠ABD,
在Rt△EBA与Rt△DBM中,
|
∴Rt△EBA≌Rt△DBM(ASA),
∴DM=EA=
| 4 |
| 3 |
∵CM=OC-OM=3-2=1,
∴CD=DM+CM=
| 7 |
| 3 |
(3)∵D(1,0),
∴CD=3-1=2,
①DC=DP,Q的横坐标为1,当x=1时,y=-
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
②DP=CP,Q的横坐标为2,当x=2时,y=-
| 2 |
| 3 |
| 4 |
| 3 |
③CD=CP,Q的横坐标为3,当x=3时,y=-
| 2 |
| 3 |
| 4 |
| 3 |
综上所述,Q的坐标为(1,
| 8 |
| 3 |
点评:此题主要考查了二次函数的综合题目,待定系数法求二次函数解析式以及利用等腰三角形的性质是解决问题的关键,注意分类思想的运用.

练习册系列答案
相关题目
下列分式的运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
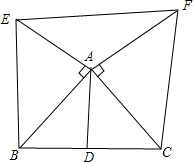 已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.
已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.
 如图,四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,则∠DBC的大小=
如图,四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,则∠DBC的大小=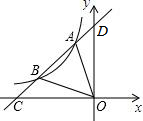 如图,一次函数y=kx+4的图象与反比例函数y=
如图,一次函数y=kx+4的图象与反比例函数y=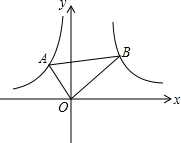 如图,在函数y=-
如图,在函数y=-