题目内容
通分:
、
和
.
| 3x |
| x2-2x |
| 2x+1 |
| 4-x2 |
| 3 |
| 2x2+4x |
考点:通分
专题:
分析:首先求出每个分式的最简公分母为2x(x+2)(x-2),运用分式的基本性质通分即可解决问题.
解答:解:∵x2-2x=x(x-2),4-x2=-(x+2)(x-2),2x2+4x=2x(x+2),
∴三个分式的最简公分母为:2x(x+2)(x-2),
∴
=
=
=
,
=-
=
=
,
=
=
=
.
∴三个分式的最简公分母为:2x(x+2)(x-2),
∴
| 3x |
| x2-2x |
| 3x |
| x(x-2) |
| 3x•2(x+2) |
| 2x(x+2)(x-2) |
| 6x2+12x |
| 2x(x+2)(x-2) |
| 2x+1 |
| 4-x2 |
| 2x+1 |
| (x+2)(x-2) |
| 2x(2x+1) |
| 2x(x+2)(x-2) |
| 4x2+2x |
| 2x(x+2)(x-2) |
| 3 |
| 2x2+4x |
| 3 |
| 2x(x+2) |
| 3(x-2) |
| 2x(x+2)(x-2) |
| 3x-6 |
| 2x(x+2)(x-2) |
点评:该题主要考查了异分母分式的通分问题;解题的关键是准确求出最简公分母;对因式分解能力提出了较高的要求.

练习册系列答案
相关题目
 如图所示,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于H,HD=1,HE=2,试求BD和CE的长.
如图所示,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于H,HD=1,HE=2,试求BD和CE的长.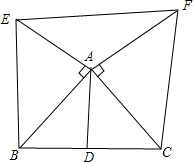 已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.
已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD. 如图,四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,则∠DBC的大小=
如图,四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,则∠DBC的大小=