题目内容
已知函数y=(m+2)x2-2x-1的图象与x轴有交点,则k的取值范围是( )
| A、m>-3 |
| B、m≥-3 |
| C、m>-3且m≠-2 |
| D、m≥-3且m≠-2 |
考点:抛物线与x轴的交点,一次函数图象上点的坐标特征,二次函数的定义
专题:分类讨论
分析:分两种情况:当m+2≠0时,抛物线与x轴的交点问题得到△=22-4(m+2)×(-1)≥0然后解不等式即可;当m+2=0时,一次函数与x轴必有交点.
解答:解:当m+2≠0时,
抛物线与x轴有交点△=22-4(m+2)×(-1)≥0,
解得m≥-3,且m≠-2;
当m+2=0时,即m=-2,
一次函数y=-2x-1的图象与x轴有交点.
因此m≥-3.
故选:B.
抛物线与x轴有交点△=22-4(m+2)×(-1)≥0,
解得m≥-3,且m≠-2;
当m+2=0时,即m=-2,
一次函数y=-2x-1的图象与x轴有交点.
因此m≥-3.
故选:B.
点评:此题考查了抛物线与x轴的交点,△=b2-4ac决定抛物线与x轴的交点个数;△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
方程
+
=0有增根,不解方程,判断这个增根是( )
| 2x |
| x-1 |
| x+k |
| 1-x |
| A、x=1 | B、x=-1 |
| C、x=±1 | D、x=0 |
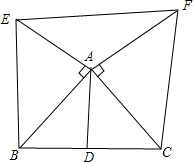 已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.
已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD. 如图,四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,则∠DBC的大小=
如图,四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,则∠DBC的大小=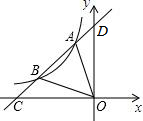 如图,一次函数y=kx+4的图象与反比例函数y=
如图,一次函数y=kx+4的图象与反比例函数y= 如图,四边形ABCD是平行四边形,E是BC的延长线上一点,AE与CD相交于F,与△CEF相似的三角形有( )个.
如图,四边形ABCD是平行四边形,E是BC的延长线上一点,AE与CD相交于F,与△CEF相似的三角形有( )个.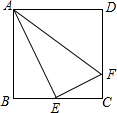 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF:CD=1:4,给出下列结论:①△ABE∽△ECF;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF.其中正确结论的序号为
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF:CD=1:4,给出下列结论:①△ABE∽△ECF;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF.其中正确结论的序号为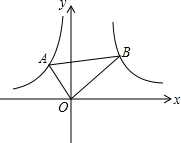 如图,在函数y=-
如图,在函数y=-